题目内容
【题目】定义:规定max(a,b)=![]() ,例如:max(﹣1,2)=2,max(3,3)=3.
,例如:max(﹣1,2)=2,max(3,3)=3.
感知:已知函数y=max(x+1,﹣2x+4)
(1)当x=3时,y=_____;
(2)当y=3时,x=______;
(3)当y随x的增大而增大时,x的取值范围为______;
(4)当﹣1≤x≤4时,y的取值范围为______;
探究:已知函数y=max(x+2,![]() )当直线y=m(m为常数)与函数y=max(x+2,
)当直线y=m(m为常数)与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
)(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
拓展:已知函数y=max(﹣x2+2nx,﹣nx)(n为常数且n≠0),当![]() n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
【答案】感知:(1)4;(2)2或![]() ;(3)x≥1;(4)2≤y≤6;探究:﹣2<m<﹣
;(3)x≥1;(4)2≤y≤6;探究:﹣2<m<﹣![]() 或4<m≤5;拓展:2≤n<6或n≤﹣6.
或4<m≤5;拓展:2≤n<6或n≤﹣6.
【解析】
感知:(1)利用题中新定义即可得到结果;
(2)利用题中新定义可对y=3所对应的的值进行分类得到两个方程,分别解方程即可求得结果;
(3)根据一次函数y=x+1和y=2x+4的图象特征,当y随x的增大而增大时,取函数y=x+1的图象部分,依题意可列出不等式,解不等式即可得出结果;
(4)根据题中新定义可列出y关于x的解析式,根据解析式和x的取值范围即可求得y的取值范围;
探究:同理(4)可得函数的解析式并画出图象,根据题意和图象即可求得m的取值范围;
拓展:先求出y=nx和y=﹣x2+2nx的图象交点,分n的情况可得函数的图象,再根据图象性质与题意列出不等式求解即可.
解:感知:(1)当x=3时,y=max(4,2),
∴y=4,
故答案为:4;
(2)当y=3时,
①当x+1=3,则x=2,此时y=max(3,0),
②当﹣2x+4=3,则x=![]() ,此时y=max(
,此时y=max(![]() ,3),
,3),
故答案为:2或![]() ;
;
(3)∵y随x的增大而增大,
∴y=x+1,
∴x+1≥﹣2x+4,
∴x≥1,
故答案为:x≥1;
(4)∵max(a,b)=![]() ,
,
当x+1<﹣2x+4时,y=﹣2x+4,此时x<1,
当x+1≥﹣2x+4时,y= x+1,此时x≥1,
∴y=![]() ,
,
∵﹣1≤x≤4,
当﹣1≤x<1时,y=﹣2x+4,此时2<y≤6,
当1≤x≤4时,y=x+1,此时2≤y≤5,
∴2≤y≤6,
故答案为:2≤y≤6;
探究:∵y=max(x+2,![]() )(﹣6<x≤3),
)(﹣6<x≤3),
同理(4)得:y= ,
,
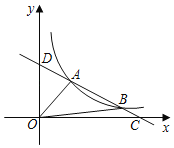
如图所示,实线部分即为其图象,

由图象可得:当﹣6<x≤﹣4时,y=m与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点,则﹣2<m≤﹣
)(﹣6<x≤3)的图象有两个公共点,则﹣2<m≤﹣![]() ;
;
当0≤x≤3时,y=m与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点,4<m≤5;
)(﹣6<x≤3)的图象有两个公共点,4<m≤5;
综上所述:﹣2<m≤﹣![]() 或4<m≤5,
或4<m≤5,
故答案为:﹣2<m≤﹣![]() 或4<m≤5;
或4<m≤5;
拓展:y=﹣x2+2nx的对称轴为x=n,
令﹣x2+2nx=﹣nx,
解得:x=0或x=3n,
∴函数y=﹣x2+2nx与y=﹣nx的交点为(0,0)和(3n,3n2),
①当n≥2时,如图1,由图象可知:0≤x≤2时,函数y=﹣x2+2nx随x值的增大而增大,
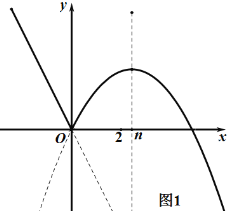
由题意得:![]() n3<0,
n3<0,
∴n<6,
∴2≤n<6;
②当n<0时,如图2,由图象可得:![]() n﹣3≥n,
n﹣3≥n,
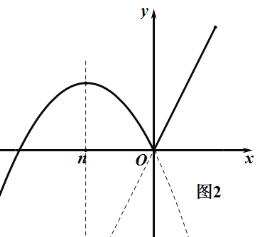
∴n≤﹣6;
综上所述:2≤n<6或n≤﹣6.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案