题目内容
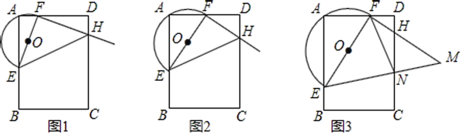
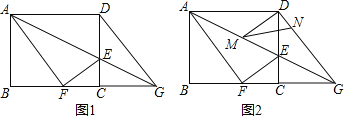
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的性质证明△ABE≌△BCF,可证得①AE⊥BF;②AE=BF正确;证明△BGE∽△ABE,可得![]() =
=![]() =
=![]() ,故③不正确;由S△ABE=S△BFC可得S四边形CEGF=S△ABG,故④正确.
,故③不正确;由S△ABE=S△BFC可得S四边形CEGF=S△ABG,故④正确.
解:在正方形ABCD中,AB=BC,∠ABE=∠C=90,
又∵BE=CF,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∴∠FBC+∠BEG=∠BAE+∠BEG=90°,
∴∠BGE=90°,
∴AE⊥BF,故①,②正确;
∵CF=2FD,BE=CF,AB=CD,
∴![]() =
=![]() ,
,
∵∠EBG+∠ABG=∠ABG+∠BAG=90°,
∴∠EBG=∠BAE,
∵∠EGB=∠ABE=90°,
∴△BGE∽△ABE,
∴![]() =
=![]() =
=![]() ,即BG=
,即BG=![]() GE,故③不正确,
GE,故③不正确,
∵△ABE≌△BCF,
∴S△ABE=S△BFC,
∴S△ABES△BEG=S△BFCS△BEG,
∴S四边形CEGF=S△ABG,故④正确.
故选:C.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目