Question

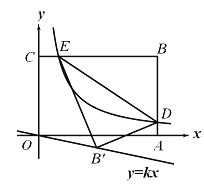
【题目】如图，平面直角坐标系中，矩形的边、分别落在、轴上，点坐标为，反比例函数的图象与边交于点，与边交于点，连结，将沿翻折至处，点恰好落在正比例函数图象上，则的值是

A. B. C. D.

Answer 1

【答案】B

【解析】试题解析：∵矩形OABC，

∴CB∥x轴，AB∥y轴，

∵点B坐标为（6，4），

∴D的横坐标为6，E的纵坐标为4，

∵D，E在反比例函数y=的图象上，

∴D（6，1），E（，4），

∴BE=6-=，BD=4-1=3，

∴ED=，

连接BB′，交ED于F，过B′作B′G⊥BC于G，

∵B，B′关于ED对称，

∴BF=B′F，BB′⊥ED，

∴BFED=BEBD，

即BF=3×，

∴BF=，

∴BB′=，

设EG=x，则BG=-x，

∵BB′2-BG2=B′G2=EB′2-GE2，

∴（）2-（-x）2=（）2-x2，

∴x=，

∴EG=，

∴CG=，

∴B′G=，

∴B′（，-），

∴k=-．

故B．