题目内容
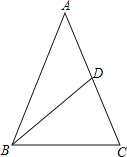
【题目】如图,已知:在△ABC中,AB=AC,BD是AC边上的中线,AB=13,BC=10,
(1)求△ABC的面积;
(2)求tan∠DBC的值.
【答案】(1)60;(2)![]() .
.
【解析】
(1)作等腰三角形底边上的高AH并根据勾股定理求出,再根据三角形面积公式即可求解;
(2)方法一:作等腰三角形底边上的高AH并根据勾股定理求出,与BD交点为E,则E是三角形的重心,再根据三角形重心的性质求出EH,∠DBC的正切值即可求出.
方法二:过点A、D分别作AH⊥BC、DF⊥BC,垂足分别为点H、F,先根据勾股定理求出AH的长,再根据三角形中位线定理求出DF的长,BF的长就等于BC的![]() ,∠DBC的正切值即可求出.
,∠DBC的正切值即可求出.
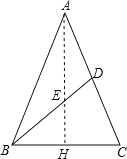
解:(1)过点A作AH⊥BC,垂足为点H,交BD于点E.
∵AB=AC=13,AH⊥BC,BC=10
∴BH=![]() 5
5
在Rt△ABH中,AH=![]() =12,
=12,
∴△ABC的面积=![]() ;
;
(2)方法一:过点A作AH⊥BC,垂足为点H,交BD于点E.

∵AB=AC=13,AH⊥BC,BC=10
∴BH=![]() 5
5
在Rt△ABH中,AH=![]() =12
=12
∵BD是AC边上的中线
所以点E是△ABC的重心
∴EH=![]() =4,
=4,
∴在Rt△EBH中,tan∠DBC=![]() =
=![]() .
.
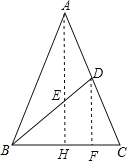
方法二:过点A、D分别作AH⊥BC、DF⊥BC,垂足分别为点H、F.
∵AB=AC=13,AH⊥BC,BC=10
∴BH=CH=![]() 5
5
在Rt△ABH中,AH=![]() =12
=12
∵AH⊥BC、DF⊥BC
∴AH∥DF,D为AC中点,
∴DF=![]() AH=6,
AH=6,![]()
∴BF=![]()
∴在Rt△DBF中,tan∠DBC=![]() =
=![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目