题目内容
如图A、B是⊙O上的两点，∠AOB=l20°，C是弧
的中点，求证四边形OACB是菱形．
 |
| AB |
证明：连OC，如图，
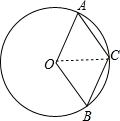∵C是弧
的中点，∠AOB=l20°
∴∠AOC=∠BOC=60°，
又∵OA=OC=OB，
∴△OAC和△OBC都是等边三角形，
∴AC=OA=OB=BC，
∴四边形OACB是菱形．
∵C是弧 |
| AB |
∴∠AOC=∠BOC=60°，
又∵OA=OC=OB，
∴△OAC和△OBC都是等边三角形，
∴AC=OA=OB=BC，
∴四边形OACB是菱形．
练习册系列答案
相关题目
