题目内容
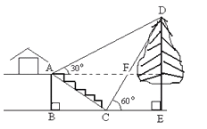
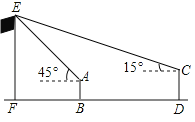
【题目】某校九(1)班开展数学活动,李明和张华两位同学合作用测角仪测量学校旗杆的高度,李明站在B点测得旗杆顶端E点的仰角为45°,张华站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知李明和张华相距(BD)30米,李明的身高(AB)1.6米,张华的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
【答案】旗杆的高![]() 为
为![]() 米.
米.
【解析】
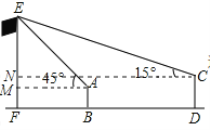
过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.15m.由李明站在B点测得旗杆顶端E点的仰角为45°,可得△AEM是等腰直角三角形,继而得出得出AM=ME,设AM=ME=xm,则CN=(x+30)m,EN=(x-0.15)m.在Rt△CEN中,由tan∠ECN=![]() ,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF.
,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF.
过点A作AM⊥EF于M,过点C作CN⊥EF于N,
∵AB=1.6,CD=1.75,
∴MN=0.15m,
∵∠EAM=45°,
∴AM=ME,
设AM=ME=xm,
则CN=(x+30)m,EN=(x-0.15)m,
∵∠ECN=15°,
∴tan∠ECN=![]() =
=![]() ,
,
即![]() ≈0.27,
≈0.27,
解得:x≈11.3,
则EF=EM+MF≈11.3+1.6=12.9(m),
答:旗杆的高![]() 为
为![]() 米.
米.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | |||||
尺寸(cm) | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 | a | 9.03 | 9.04 | 9.06 | 9.07 | 9.08 | b |
按照生产标准,产品等次规定如下:
尺寸(单位:cm) | 产品等次 |
8.97≤x≤9.03 | 特等品 |
8.95≤x≤9.05 | 优等品 |
8.90≤x≤9.10 | 合格品 |
x<8.90或x>9.10 | 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.