ЬтФПФкШн
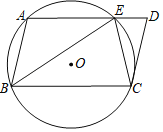
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+3гыxжсНЛгкA(1ЃЌ0)ЁЂB(Љ3ЃЌ0)СНЕуЃЌгыyжсНЛгкЕуCЃЌЩшХзЮяЯпЕФЖЅЕуЮЊDЃЎ
(1)ЧѓИУХзЮяЯпЕФНтЮіЪНгыЖЅЕуDЕФзјБъЃЎ
(2)ЪдХаЖЯЁїBCDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
(3)ШєЕуEдкxжсЩЯЃЌЕуQдкХзЮяЯпЩЯЃЎЪЧЗёДцдквдBЁЂCЁЂEЁЂQЮЊЖЅЕуЧввдBCЮЊвЛБпЕФЦНааЫФБпаЮЃПШєДцдкЃЌжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
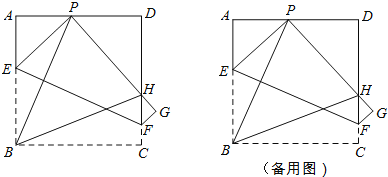
(4)ЬНОПзјБъжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУвдPЁЂAЁЂCЮЊЖЅЕуЕФШ§НЧаЮгыЁїBCDЯрЫЦЃПШєДцдкЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
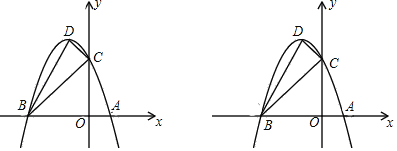
ЁОД№АИЁП(1) ХзЮяЯпЕФНтЮіЪНЮЊyЃНЉx2Љ2x+3ЃЌЖЅЕуDЕФзјБъЮЊ(Љ1ЃЌ4)ЃЛ(2) ЁїBCDЪЧжБНЧШ§НЧаЮЃЌРэгЩМћНтЮіЃЛ(3) QЕуЕФзјБъЮЊ(Љ2ЃЌ3)Лђ(![]() Љ1ЃЌЉ3)Лђ(Љ
Љ1ЃЌЉ3)Лђ(Љ![]() Љ1ЃЌЉ3)ЃЛ (4) ЗћКЯЬѕМўЕФЕуPЕФзјБъЮЊЃК(0ЃЌ0)Лђ(0ЃЌЉ
Љ1ЃЌЉ3)ЃЛ (4) ЗћКЯЬѕМўЕФЕуPЕФзјБъЮЊЃК(0ЃЌ0)Лђ(0ЃЌЉ![]() )Лђ(Љ9ЃЌ0)ЃЎ
)Лђ(Љ9ЃЌ0)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉРћгУЙДЙЩЖЈРэЧѓЕУЁїBCDЕФШ§БпЕФГЄЃЌШЛКѓИљОнЙДЙЩЖЈРэЕФФцЖЈРэМДПЩзїГіХаЖЯЃЛ
ЃЈ3ЃЉЕБBЁЂCЁЂEЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌгаСНжжЧщПіЃКЂйЕБQЕуЕФзнзјБъЮЊ3ЪБЃЌЂкЕБЕуQЕФзнзјБъЉ3ЪБЃЌДњШыНтЮіЪНМДПЩЧѓЕУЃЛ
ЃЈ4ЃЉЗжPдкxжсКЭyжсСНжжЧщПіЬжТлЃЌЩсГіPЕФзјБъЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпЕФБШЯрЕШМДПЩЧѓНтЃЎ
(1)ХзЮяЯпyЃНax2+bx+3гыxжсНЛгкA(1ЃЌ0)ЁЂB(Љ3ЃЌ0)СНЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУaЃНЉ1ЃЌbЃНЉ2ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНЉx2Љ2x+3ЃЌ
ЁпyЃНЉx2Љ2x+3ЃНЉ(x+1)2+4ЃЌ
ЁрЖЅЕуDЕФзјБъЮЊ(Љ1ЃЌ4)ЃЛ
(2)ЁїBCDЪЧжБНЧШ§НЧаЮЃЎ
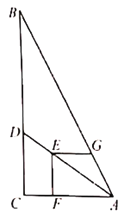
РэгЩШчЯТЃКШчЭМ1ЃЌЙ§ЕуDЗжБ№зїxжсЁЂyжсЕФДЙЯпЃЌДЙзуЗжБ№ЮЊEЁЂFЃЌ

ЁпдкRtЁїBOCжаЃЌOBЃН3ЃЌOCЃН3ЃЌ
ЁрBC2ЃНOB2+OC2ЃН18ЃЌ
дкRtЁїCDFжаЃЌDFЃН1ЃЌCFЃНOFЉOCЃН4Љ3ЃН1ЃЌ
ЁрCD2ЃНDF2+CF2ЃН2ЃЌ
дкRtЁїBDEжаЃЌDEЃН4ЃЌBEЃНOBЉOEЃН3Љ1ЃН2ЃЌ
ЁрBD2ЃНDE2+BE2ЃН20ЃЌ
ЁрBC2+CD2ЃНBD2
ЁрЁїBCDЮЊжБНЧШ§НЧаЮЃЛ
(3)ЂйЕБQЕуЕФзнзјБъЮЊ3ЪБЃЌ
ЁрАбyЃН3ДњШыyЃНЉx2Љ2x+3ЧѓЕУxЃН0ЛђЉ2ЃЌ
ЁрQ1(Љ2ЃЌ3)ЃЛ
ЂкЕБQЕуЕФзнзјБъЮЊЉ3ЪБЃЌ
АбyЃНЉ3ДњШыyЃНЉx2Љ2x+3ЧѓЕУxЃН![]() Љ1ЛђЉ
Љ1ЛђЉ![]() Љ1ЃЌ
Љ1ЃЌ
ЁрQ2(![]() Љ1ЃЌЉ3)ЃЌQ3(Љ
Љ1ЃЌЉ3)ЃЌQ3(Љ![]() Љ1ЃЌЉ3)ЃЌ
Љ1ЃЌЉ3)ЃЌ
злЩЯЃЌQЕуЕФзјБъЮЊ(Љ2ЃЌ3)Лђ(![]() Љ1ЃЌЉ3)Лђ(Љ
Љ1ЃЌЉ3)Лђ(Љ![]() Љ1ЃЌЉ3)ЃЎ
Љ1ЃЌЉ3)ЃЎ
(4)гЩ(2)жЊBCЃН3![]() ЃЌCDЃН
ЃЌCDЃН![]() ЃЌBDЃН2
ЃЌBDЃН2![]() ЃЌ
ЃЌ
ЂйЁп![]() ЃЌ
ЃЌ![]() ЃЌЙЪЕБPЪЧдЕуOЪБЃЌЁїACPЁзЁїDBCЃЛ
ЃЌЙЪЕБPЪЧдЕуOЪБЃЌЁїACPЁзЁїDBCЃЛ
ЂкЕБACЪЧжБНЧБпЪБЃЌШєACгыCDЪЧЖдгІБпЃЌ
ЩшPЕФзјБъЪЧ(0ЃЌa)ЃЌдђPCЃН3ЉaЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКaЃНЉ9ЃЌ
дђPЕФзјБъЪЧ(0ЃЌЉ9)ЃЌШ§НЧаЮACPВЛЪЧжБНЧШ§НЧаЮЃЌдђЁїACPЁзЁїCBDВЛГЩСЂЃЛ
ЂлЕБACЪЧжБНЧБпЃЌШєACгыBCЪЧЖдгІБпЪБЃЌ
ЩшPЕФзјБъЪЧ(0ЃЌb)ЃЌдђPCЃН3ЉbЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКbЃНЉ![]() ЃЌ
ЃЌ
ЙЪPЪЧ(0ЃЌЉ![]() )ЪБЃЌдђЁїACPЁзЁїCBDвЛЖЈГЩСЂЃЛ
)ЪБЃЌдђЁїACPЁзЁїCBDвЛЖЈГЩСЂЃЛ
ЂмЕБPдкxжсЩЯЪБЃЌACЪЧжБНЧБпЃЌPвЛЖЈдкBЕФзѓВрЃЌЩшPЕФзјБъЪЧ(dЃЌ0)ЃЌ
дђAPЃН1ЉdЃЌЕБACгыCDЪЧЖдгІБпЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКdЃН1Љ3![]() ЃЌДЫЪБЃЌСНИіШ§НЧаЮВЛЯрЫЦЃЛ
ЃЌДЫЪБЃЌСНИіШ§НЧаЮВЛЯрЫЦЃЛ
ЂнЕБPдкxжсЩЯЪБЃЌACЪЧжБНЧБпЃЌPвЛЖЈдкBЕФзѓВрЃЌЩшPЕФзјБъЪЧ(eЃЌ0)ЃЎ
дђAPЃН1ЉeЃЌЕБACгыDCЪЧЖдгІБпЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКeЃНЉ9ЃЌЗћКЯЬѕМўЃЎ
злЩЯЃЌЗћКЯЬѕМўЕФЕуPЕФзјБъЮЊЃК(0ЃЌ0)Лђ(0ЃЌЉ![]() )Лђ(Љ9ЃЌ0)ЃЎ
)Лђ(Љ9ЃЌ0)ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ