题目内容
【题目】如图，在等腰三角形ACB中，AC＝BC＝10，AB＝16，D为底边AB上一动点(不与点A，B重合)，DE⊥AC，DF⊥BC，垂足分别为点E，F，则DE+DF等于_____．
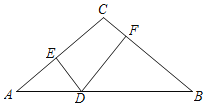
【答案】9.6
【解析】
连接CD，过C点作底边AB上的高CG，根据等腰三角形的性质得出BG＝8，利用勾股定理求出CG＝6，再根据S△ABC＝S△ACD+S△DCB不难求得DE+DF的值．
连接CD，过C点作底边AB上的高CG，
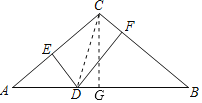
∵AC＝BC＝10，AB＝16，
∴BG＝
AB＝8，CG＝
＝
＝6，
∵S△ABC＝S△ACD+S△DCB，
∴ABCG＝ACDE+BCDF，
∵AC＝BC，
∴16×6＝10×(DE+DF)，
∴DE+DF＝9.6．
故答案为：9.6．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
