题目内容
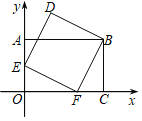
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图像上.
的图像上.
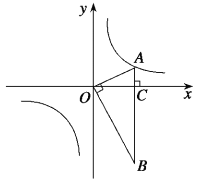
(1)k= ;
(2)在x轴的负半轴上存在一点 P ,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE,直接写出点E的坐标,并判断点E是否在该反比例函数的图像上,说明理由.
【答案】(1)![]() ;(2)点P的坐标为(-2
;(2)点P的坐标为(-2![]() ,0). (3)点E在该反比例函数的图象上,理由见解析.
,0). (3)点E在该反比例函数的图象上,理由见解析.
【解析】
(1)把A的坐标代入反比例函数的表达式,即可求出答案;
(2)根据C点的坐标求出OC、AC的长,可证得△OAC∽△BOC,由相似三角形对应边成比例列出比例式求出BC的长,然后根据三角形面积公式求出△OAB的面积,根据已知S△AOP=![]() S△AOB,求出OP长,即可求出答案;
S△AOB,求出OP长,即可求出答案;
(3)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(-![]() ,-1),即可求解.
,-1),即可求解.
解:(1)把A(![]() ,1)代入反比例函数y=
,1)代入反比例函数y=![]() 得:k=1×
得:k=1×![]() =
=![]() ;
;
(2)∵A(![]() ,1),AB⊥x轴于点C,∴OC=
,1),AB⊥x轴于点C,∴OC=![]() ,AC=1.
,AC=1.
∵OA⊥OB,AB⊥x轴,
∴△OAC∽△BOC,
∴OC2=AC·BC,
可得BC=3,
∴B(![]() ,-3),AB=4,
,-3),AB=4,
∴S△AOB=![]() ×
×![]() ×4=2
×4=2![]() ,∴S△AOP=
,∴S△AOP=![]() S△AOB=
S△AOB=![]() ,
,
设点P的坐标是为(m,0),∴![]() ×|m|×1=
×|m|×1=![]() ,∴|m|=2
,∴|m|=2![]() .
.
∵P是x轴负半轴上的点,
∴m=-2![]() ,
,
即点P的坐标为(-2![]() ,0).
,0).
(3)点E在该反比例函数的图象上,理由如下:
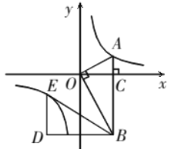
∵OA⊥OB,OA=2,OB=2![]() ,AB=4,
,AB=4,
∴sin∠ABO=![]() =
=![]() =
=![]() ,
,
∴∠ABO=30°.
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴∠OBD=60°,BO=BD=2![]() ,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°.
,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°.
又BD-OC=![]() ,BC-DE=1,
,BC-DE=1,
∴E(-![]() ,-1),
,-1),
而(-1)×(-![]() )=
)=![]() .
.
∴点E在该反比例函数的图象上.

【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
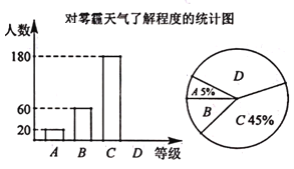
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).
【题目】某市农林种植专家指导贫困户种植红梨和青枣,收获的红梨和青枣优先进入该市水果市场.已知某水果经销商购进了红梨和青枣两种水果各10箱,分配给下属的甲、乙两个零售店(分别简称甲店、乙店)销售.预计每箱水果的盈利情况如表
红梨/箱 | 青枣/箱 | |
甲店 | 22元 | 34元 |
乙店 | 18元 | 26元 |
(1)若甲、乙两店各配货10箱,其中甲店配红梨2箱,青枣8箱;乙店配红梨8箱,青枣2箱,请你计算出经销商能盈利多少元?
(2)若甲、乙两店各配货10箱,且在保证乙店盈利不小于200元的条件下,请你设计出使水果经销商盈利最大的配货方案.