题目内容
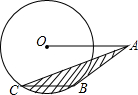
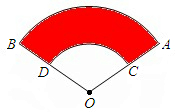
如图，在△OAB中，OA=OB=2，∠OAE=30°，⊙O上的E点是△OAB的边AB的中点，⊙O分别交OA、OB于C、D，求图中阴影部分的面积（结果保留字母π）．
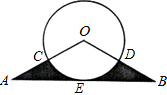
连接OE，
∵OA=OB，E点是AB的中点，
∴OE⊥AB，
∴AB是⊙O的切线，
，
∵∠OAE=30°，OA=OB=2，
∴OE=1，AE=
，∠AOB=120°，
∴AB=2
，
S阴影部分的面积=S△AOB-S扇形OCD=
AB×OE-
=
-
π．
∵OA=OB，E点是AB的中点，
∴OE⊥AB，
∴AB是⊙O的切线，
，∵∠OAE=30°，OA=OB=2，
∴OE=1，AE=
| 3 |
∴AB=2
| 3 |
S阴影部分的面积=S△AOB-S扇形OCD=
| 1 |
| 2 |
| 120π×12 |
| 360 |
| 3 |
| 1 |
| 3 |
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
