题目内容
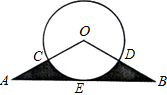
如图,菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O按顺时针方向旋转90°,则图中阴影部分的面积是______.


连接OB、OB′,过点A作AN⊥BO于点N,
菱形OABC中,∠A=120°,OA=1,
∴∠AOC=60°,∠COA′=30°,
∴AN=
,
∴NO=
=
,
∴BO=
,
∴S△CBO=S△C′B′O=
×
AO•2CO•sin60°=
,
S扇形OCA′=
=
,
S扇形OBB′=
=
;
∴阴影部分的面积=
-(2×
+
)=
π-
.
故答案为:
π-
.
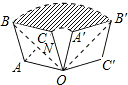
菱形OABC中,∠A=120°,OA=1,
∴∠AOC=60°,∠COA′=30°,
∴AN=
| 1 |
| 2 |
∴NO=
12-(
|
| ||
| 2 |
∴BO=
| 3 |
∴S△CBO=S△C′B′O=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
S扇形OCA′=
| 30π×1 |
| 360 |
| π |
| 12 |
S扇形OBB′=
90π(
| ||
| 360 |
| 3π |
| 4 |
∴阴影部分的面积=
| 3π |
| 4 |
| ||
| 4 |
| π |
| 12 |
| 2 |
| 3 |
| ||
| 2 |
故答案为:
| 2 |
| 3 |
| ||
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目