题目内容
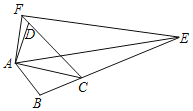
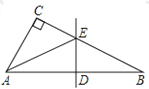
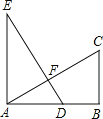
【题目】如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB中点,在“①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°”这四个结论中,正确的个数有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据点D是AB的中点,得到AD=![]() ,由于AB=2BC,于是得到AD=BC,证得Rt△AED≌Rt△BAC,得到∠E=∠CAB,DE=AC,故①正确;由∠E+∠EDA=90°,得到∠FAD+∠EDA=90°,即可得到DE⊥AC,故②正确;根据同角的余角相等得到∠EAF=∠ADE,故③正确;根据BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,故④错误.
,由于AB=2BC,于是得到AD=BC,证得Rt△AED≌Rt△BAC,得到∠E=∠CAB,DE=AC,故①正确;由∠E+∠EDA=90°,得到∠FAD+∠EDA=90°,即可得到DE⊥AC,故②正确;根据同角的余角相等得到∠EAF=∠ADE,故③正确;根据BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,故④错误.
解:
点D是AB的中点,则AD=![]() ,
,
∵AB=2BC,
∴AD=BC,
∵EA⊥AB,CB⊥AB,
∴∠B=∠EAB=90°,
在△AED与△BAC中, ,
,
∴△AED≌△BAC,
∴∠E=∠CAB,DE=AC,
∴①正确;
∵∠E+∠EDA=90°,
∴∠FAD+∠EDA=90°,
∴∠AFD=180°-(∠FAD+∠EDA)=90°,
∴DE⊥AC,
∴②正确;
∵∠EAF与∠ADE都是∠E的余角,
∴∠EAF=∠ADE,
∴③正确;
∵BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,
∴④错误;
故选:C.

【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.