题目内容
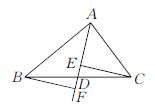
【题目】在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,CE=2cm.
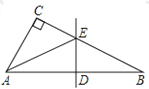
求:(1)∠AEB 度数.
(2)BC的长.
【答案】见解析
【解析】
(1)根据DE垂直平分斜边AB,可得EA=EB,从而∠EAB=∠B,结合条件可求出∠CAE=30°,然后可求∠AEB 度数;
(2)在△ACE中,∠C=90°,∠CAE=30°,所以AE=2CE=4,而AE=BE,BC=CE+BE=6.
(1)解:∵DE垂直平分斜边AB
∴EA=EB
∴∠EAB=∠B
∵∠CAB=∠B+30°且∠CAB=∠CAE+∠EAB
∴∠CAE=30°
∴∠AEB=∠CAE+∠C=30°+90°=120°
(2)在△ACE中,
∵∠C=90°,∠CAE=30°,
∴AE=2CE=4,
又∵AE=BE,
∴BC=CE+BE=6cm.

练习册系列答案
相关题目