Question

【题目】已知：点为边上的一个动点．

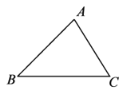
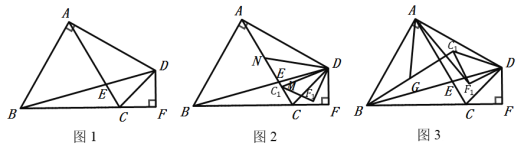
（1）如图1，若是等边三角形，以为边在的同侧作等边，连接．试比较与的大小，并说明理由；

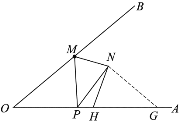
（2）如图2，若中，，以为底边在的同侧作等腰，且∽，连接．试判断与的位置关系，并说明理由；

Answer 1

【答案】（1）∠DAC＝∠B，理由见解析；（2）AD∥BC，理由见解析

【解析】

（1）首先根据等边三角形性质得出BC=AC，DC=EC，∠ACB=∠DCE=60°，从而进一步证明出∠DCA=∠ECB，最后通过证明，由此证明结论即可；

（2）首先根据相似三角形性质得出＝，从而得出＝，紧接着根据题意通过证明得出∠DAC＝∠EBC，进一步证明∠DAC=∠ACB，由此即可证明出AD∥BC.

（1）∠DAC＝∠B，

理由如下：

∵和都是等边三角形，

∴BC=AC，DC=EC，∠ACB=∠DCE=60°，

∴∠BCE+∠ACE＝∠ACD+∠ACE，

∴∠BCE＝∠ACD，

在和中，

∵，

∴，

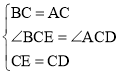∴∠B＝∠DAC；

（2）AD∥BC，

理由如下：

∵，

∴＝，

∴＝，

由可得：∠DCE＝∠ACB，

∴∠DCA+∠ACE＝∠ECB+∠ACE，

∴∠DCA＝∠ECB，

∴，

∴∠DAC＝∠EBC，

∵是等腰三角形，

∴∠EBC＝∠ACB，

∴∠DAC=∠ACB，

∴AD∥BC．