Question

【题目】ABC为等边三角形，以AB边为腰作等腰RtABD，∠BAD=90，AC与BD交于点E，连接CD，过点D作DF⊥BC交BC延长线于点F．

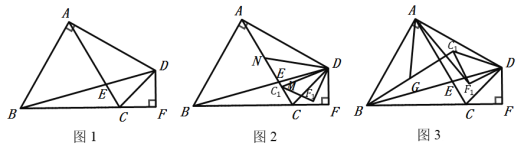
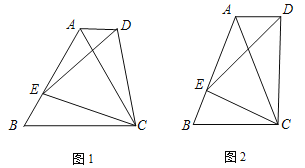
（1）如图1，若DF＝1，AB= ；AE= ；

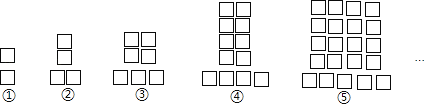
（2）如图2，将CDF绕点D顺时针旋转至△C1DF1的位置，点C，F的对应点分别为C1，F1，当DC1平分∠EDC时，DC1与AC交于点M，在AM上取点N，使AN＝DM，连接DN，求tan∠NDM的值．

（3）如图3，将CDF绕点D顺时针旋转至C1DF1的位置，点C，F的对应点分别为C1，F1，连接AF1、BC1，点G是BC1的中点，连接AG．求的值；

Answer 1

【答案】（1）AB=，AE=2；（2）tan∠NDM=；（3）=

【解析】

（1）作AM⊥BC于M，AN⊥DF于N，EH⊥AB于H，在BF上取一点K，使得BK=DK，先证明四边形AMFN是正方形，然后可推出Rt△ACM≌Rt△AND，可得CM=DN，CF=DF=1，根据∠ABC=60°，得出∠ABD=45°，∠KBD=∠KDB=15°，∠DKF=∠KBD+∠KDB=30°，可得出KD=KB=2，KF=，即可推出BF=2+，BC=AB=+1，设AE=x，则AH=x，BH=HE=x，即可求出AE；

（2）先证明∠DEC＝∠DCE＝75°，然后根据等腰三角形的性质得出DM⊥AM，推出∠AMD＝90°，∠ADM＝60°，设DM＝AN＝a，可得AM＝a，NM＝（1）a，即可得出答案；

（3）延长FG到M，延长BA交F1C1的延长线于N，使得GM=F1G，则△GMB≌△GF1C1，可推出∠MBA=∠N，然后证明△ABM≌△ADF1，可推出△AMF1是等腰直角三角形，AG⊥MF1，AG=GF1，即可证明结论．

（1）如图1中，作AM⊥BC于M，AN⊥DF于N，EH⊥AB于H，在BF上取一点K，使得BK=DK，

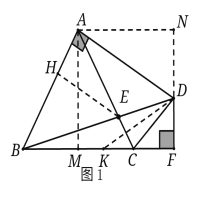
∵∠BAD=∠BFD=90°，

∴∠BAD+∠BFD=180°，

∴∠ABF+∠ADF=180°，

∵∠ABC=60°，

∴∠ADF=120°，

∴∠ADN=60°，

∴△AMB≌△AND(AAS)，

∴AM=AN，

∵四边形AMFN是矩形，

∴四边形AMFN是正方形，

∴FM=FN，

∴Rt△ACM≌Rt△AND，

∴CM=DN，

∴CF=DF=1，

∵∠ABC=60°，

∴∠ABD=45°，

∴∠KBD=∠KDB=15°，

∴∠DKF=∠KBD+∠KDB=30°，

∴KD=KB=2，KF=，

∴BF=2+，BC=AB=+1，

设AE=x，则AH=x，BH=HE=x，

∴x+x=+1，

解得x=2，

∴AE=2，

故答案为：AB=+1，AE=2；

（2）∵∠BAD＝90°，∠BAC＝60°，

∴∠CAD＝90°60°＝30°，

∵△ABC为等边三角形，△ABD为等腰直角三角形，

∴∠EAD=30°，∠ADB=45°，∠ACB=60°，

∴∠DEC=75°，

由（1）可得CF=DF，

∴∠DCF=45°，

∴∠DCE=180°-∠ACB-∠DCF=75°，

∵∠DEC＝∠DCE＝75°，

∴DE＝DC，

∵DC1平分∠EDC，

∴DM⊥AM，

∴∠AMD＝90°，∠ADM＝60°，

设DM＝AN＝a，易知AM＝a，NM＝（1）a，

∴tan∠NDM==；

（3）如图3，延长FG到M，延长BA交F1C1的延长线于N，使得GM=F1G，则△GMB≌△GF1C1，

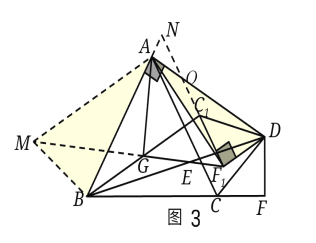
∴BM=F1C1=DF1，∠BMG=∠GF1N，

∴BM//F1N，

∴∠MBA=∠N，

∵∠NAO=∠OF1D=90°，∠AON=∠DOF1，

∴∠N=∠ADF1，

∴∠ABM=∠ADF1，

∵AB=AD，

∴△ABM≌△ADF1，

∴AM=AF1，∠MAB=∠DAF1，

∴∠MAF1=∠BAD=90°，

∴△AMF1是等腰直角三角形，

∴AG⊥MF1，AG=GF1，

∴AF1=AG，即=．