题目内容
【题目】已知在扇形![]() 中,圆心角
中,圆心角![]() ,半径
,半径![]() .
.
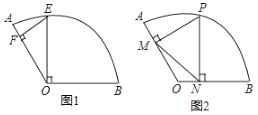
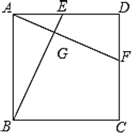
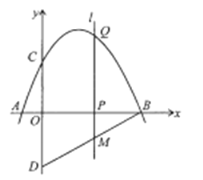
(1)如图1,过点![]() 作
作![]() ,交弧
,交弧![]() 于点
于点![]() ,再过点
,再过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 的长为_________,
的长为_________,![]() 的度数为_________;
的度数为_________;
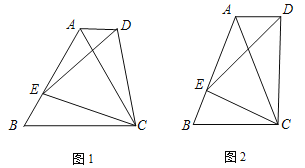
(2)如图2,设点![]() 为弧
为弧![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 分别在半径
分别在半径![]() ,
,![]() 上,连接
上,连接![]() ,则
,则
①求点![]() 运动的路径长是多少?
运动的路径长是多少?
②![]() 的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
(3)在(2)中的条件下,若点![]() 是
是![]() 的外心,直接写出点
的外心,直接写出点![]() 运动的路经长.
运动的路经长.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②是定值,为
;②是定值,为![]() ;(3)
;(3)![]()
【解析】
(1)先求出∠AOE,再解直角三角形,即可得出结论;
(2)①当点M与点O重合时,∠PMB=30°,当点N与点O重合时,∠PNA=30°,进而求出点P运动路径所对的圆心角是120°-30°-30°=60°,最后用弧长公式即可得出结论;
②先判断出点P,M,O,N四点均在同一个圆,即⊙H上,进而求出MK=![]() ,即可得出结论;
,即可得出结论;
(3)先判断出三角形PMN的外接圆的圆心的运动轨迹,最后根据弧长公式即可得出结论.
解:(1)∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() .
.
∴![]() ,
,![]() ,
,
故答案为:![]() ,
,![]()
(2)①点![]() 在弧
在弧![]() 上运动,其路径也是一段弧,由题意可知,
上运动,其路径也是一段弧,由题意可知,
当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,
当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,
∴点![]() 运动路径所对的圆心角是
运动路径所对的圆心角是![]() ,
,
∴点![]() 运动的路径长
运动的路径长![]() ;
;
②是定值;
连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵在![]() 和
和![]() 中,点
中,点![]() 是斜边
是斜边![]() 的中点,
的中点,
∴![]() ,
,
∴根据圆的定义可知,点![]() 四点均在同一个圆,即
四点均在同一个圆,即![]() 上,
上,
又∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
由垂径定理得,![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,是定值.
,是定值.
(3)由(2)知,点![]() 四点共圆,
四点共圆,
∴![]() 是
是![]() 的外接圆的圆心,即:点
的外接圆的圆心,即:点![]() 和点
和点![]() 重合,
重合,
∴![]() ,
,
∴点![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径,
为半径,
∴点![]() 运动路径所对的圆心角是
运动路径所对的圆心角是![]() ,
,
∴点![]() 运动路径所对的圆心角是
运动路径所对的圆心角是![]() ,
,
∴点![]() 运动的路经长为
运动的路经长为![]() .
.

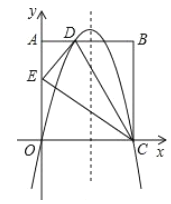
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
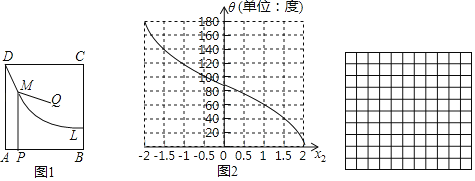
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
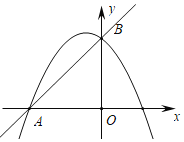
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .