题目内容
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m,坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E、A、C在同一水平线上,求建筑物BC的高.(结果保留整数,参考数据tan50°=1.1918,cos50°=0.6428)

【答案】建筑物BC的高约为21m
【解析】分析:过点D作DM⊥BC于点M,DN⊥AC于点N,则四边形DMCN是矩形,DH=EC,DE=HC,设建筑物BC的高度为xm,则BH=(x-5)m,由三角函数得出DH=![]() (x-5),AC=EC-EA=
(x-5),AC=EC-EA=![]() (x-5)-10,得出x=tan50°[
(x-5)-10,得出x=tan50°[![]() (x-5)],解方程即可.
(x-5)],解方程即可.
本题解析:
过点D作DM⊥BC于点M,DN⊥AC于点N,如图所示:
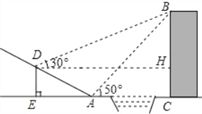
则四边形DMCN是矩形,DH=EC,DE=HC,设建筑物BC的高度为xm,则BH=(x﹣5)m,
在Rt△DHB中,∠BDH=30°,∴DH=![]() (x﹣5),AC=EC﹣EA=
(x﹣5),AC=EC﹣EA=![]() (x﹣5)﹣10,
(x﹣5)﹣10,
在Rt△ACB中,∠BAC=50°,tan∠BAC=![]() ,∴x=tan50°[
,∴x=tan50°[![]() (x﹣5)],
(x﹣5)],
解得:x≈21,答:建筑物BC的高约为21m.

练习册系列答案
相关题目
【题目】如图,自行车每节链条的长度为![]() ,交叉重叠部分的圆的直径为
,交叉重叠部分的圆的直径为![]() .
.
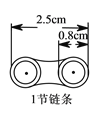


(![]() )观察图形,填写下表:
)观察图形,填写下表:
链条的节数/节 |
|
|
|
|
链条的长度/ |
|
(![]() )如果
)如果![]() 节链条的长度是
节链条的长度是![]() ,那么
,那么![]() 与
与![]() 之间的关系式是什么?
之间的关系式是什么?
(![]() )如果一辆某种型号自行车的链条(安装前)由
)如果一辆某种型号自行车的链条(安装前)由![]() 节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?