题目内容
已知抛物线C1:y=
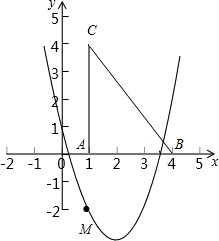
(x+2)2-5的顶点为P,与x轴正半轴交于点B,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式.

| 5 |
| 9 |

点P的坐标为(-2,-5),
令y=0,则
(x+2)2-5=0,
解得x1=1,x2=-5,
所以,点B的坐标为(1,0),
∵点P、M关于点B对称,
∴点M的坐标为(4,5),
∵抛物线C2与抛物线C1关于x轴对称,抛物线C2向右平移得到C3,
∴抛物线C3的解析式为y=-
(x-4)2+5.
令y=0,则
| 5 |
| 9 |
解得x1=1,x2=-5,
所以,点B的坐标为(1,0),
∵点P、M关于点B对称,
∴点M的坐标为(4,5),
∵抛物线C2与抛物线C1关于x轴对称,抛物线C2向右平移得到C3,
∴抛物线C3的解析式为y=-
| 5 |
| 9 |

练习册系列答案
相关题目