题目内容
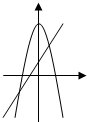
若二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).则S=a+b+c的值的变化范围是______.
将点(0,1)和(-1,0)分别代入抛物线解析式,得c=1,a=b-1,
∴S=a+b+c=2b,
由题设知,对称轴x=-
>0且a<0,
∴2b>0.
又由b=a+1及a<0可知2b=2a+2<2.
∴0<S<2.
故本题答案为:0<S<2.
∴S=a+b+c=2b,
由题设知,对称轴x=-
| b |
| 2a |
∴2b>0.
又由b=a+1及a<0可知2b=2a+2<2.
∴0<S<2.
故本题答案为:0<S<2.

练习册系列答案
相关题目