题目内容
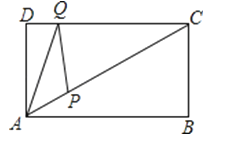
【题目】如图,矩形ABCD中,AB=8,AD=5,点E![]() 为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.

【答案】![]() 或
或![]()
【解析】分析:过点D′作MN⊥AB于点N,MN交CD于点M,由矩形有两条对称轴可知要分两种情况考虑,根据对称轴的性质以及折叠的特性可找出各边的关系,在直角△EMD′与△AND′中,利用勾股定理可得出关于DM长度的一元二次方程,解方程即可得出结论.
详解:过点D′作MN⊥AB于点N,MN交CD于点M,如图1、所示.
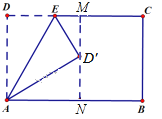
设DE=a,则D′E=a.
∵矩形ABCD有两条对称轴,
∴分两种情况考虑:
①当DM=CM时,
AN=DM=![]() CD=
CD=![]() AB=4,AD=AD′=5,
AB=4,AD=AD′=5,
由勾股定理可知:
ND′=![]() ,
,
∴MD′=MN-ND′=AD-ND′=2,EM=DM-DE=4-a,
∵ED′2=EM2+MD′2,即a2=(4-a)2+4,
解得:a=![]() ;
;
②当MD′=ND′时,
MD′=ND′=![]() MN=
MN=![]() AD=
AD=![]() ,
,
由勾股定理可知:
AN=![]() ,
,
∴EM=DM-DE=AN-DE=![]() -a,
-a,
∵ED′2=EM2+MD′2,即a2=(![]() a)2+(
a)2+(![]() )2,
)2,
解得:a=![]() .
.
综上知:DE=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() ..
..

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目