��Ŀ����
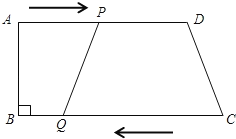
����Ŀ����ͼ��ʾ��������ABCD�У�AD��BC����B=90�㣬AD=24cm��BC=26cm������P�ӵ�A������AD�������D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ����CB�������B��3cm/s���ٶ��˶�����P��Q�ֱ�ӵ�A�͵�Cͬʱ������������һ�㵽��˵�ʱ����һ����ֹ֮ͣ�˶���
��1�������ʱ�䣬�ı���PQCD��ƽ���ı��Σ�
��2�������ʱ�䣬�ı���PQBA�Ǿ��Σ�
��3�������ʱ�䣬��PQ��ƽ����CDʱ����PQ=CD��

���𰸡���1��6�룻��2��6.5�룻��3��7��.
����������������1���辭��tsʱ���ı���PQCD��ƽ���ı��Σ�����DP=CQ�������������ɣ�
��2���辭��tsʱ���ı���PQBA�Ǿ��Σ�����AP=BQ�������������ɣ�
��3���辭��t��s�����ı���PQCD�ǵ������Σ�����EP=2�г��й�t�ķ�����⼴�ɣ�
��⣺��1���辭��x�룬�ı���PQCDΪƽ���ı���
��PD=CQ
����24��x=3x��
��ã�x=6��
��2���辭��y�룬�ı���PQBAΪ���Σ�
��AP=BQ��
����y=26��3y��
��ã�y=![]() ��
��
��3���辭��t�룬�ı���PQCD�ǵ������Σ�
��P����PE��AD����D����DF��BC��
���QEP=��DFC=90��
���ı���PQCD�ǵ������Σ�
��PQ=DC��
�֡�AD��BC����B=90�㣬
��AB=PE=DF��
��Rt��EQP��Rt��FCD��
PQ=DC
PE=DF
��Rt��EQP��Rt��FCD��HL����
��EQ=FC
��FC=BC��AD=26��24=2��
�֡�BQ=BC-CQ=26��3t��
��EQ=AP��BQ=t����26��3t��=4t-26��
��4t-26=2
�ã�t=7��
�ྭ��7s��PQ=CD��

 ������������ϵ�д�
������������ϵ�д�





