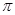题目内容
如图，PA、PB是⊙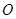
的切线，切点分别是A、B，若∠APB=60°，PA=4．则⊙⊙的半径是__________．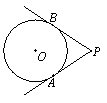
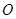的切线，切点分别是A、B，若∠APB=60°，PA=4．则⊙⊙的半径是__________．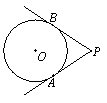
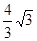
连接OA、OP，根据切线长定理即可求得∠OPA=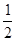 
∠APB，在Rt△OAP中利用三角函数即可求解．
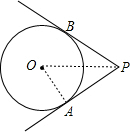
解：连接OA、OP
∵PA、PB是⊙O的切线
∴∠OAP=90°，∠APO=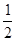∠APB=30°
Rt△OAP中，
∵tan∠APO=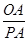
∴OA=PA?tan30°=4×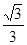
=
．
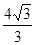本题考查了切线的性质定理，以及三角函数，正确作出直角三角形是关键．
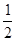∠APB，在Rt△OAP中利用三角函数即可求解．解：连接OA、OP
∵PA、PB是⊙O的切线
∴∠OAP=90°，∠APO=
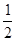∠APB=30°Rt△OAP中，
∵tan∠APO=
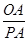
∴OA=PA?tan30°=4×
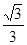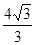=．本题考查了切线的性质定理，以及三角函数，正确作出直角三角形是关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
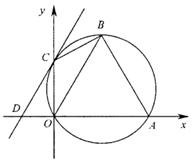
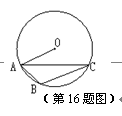
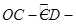线段DO的路线作匀速运动．设运动时间为
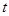秒,∠APB的度数为
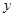度，则下列图象中表示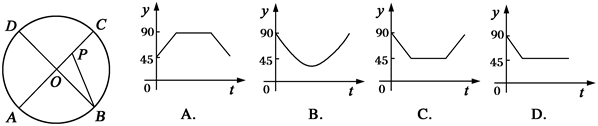
，
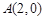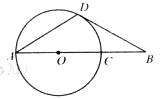
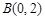，⊙C的圆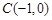
，半径为1．若D是⊙C上的一个动点，线段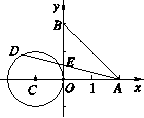
）
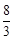
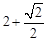