题目内容
(本小题9分)如图,在直角坐标系xoy中,点A(2,0),点B在第一象限且△OAB为等边三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D
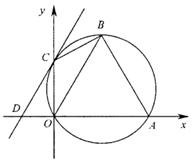
小题1:(1)判断点C是否为弧OB的中点?并说明理由;
小题2:(2)求B、C两点的坐标;
小题3:(3)求直线CD的函数解析式;
小题4:(4)点P在线段OB上,且满足四边形OPCD是等腰梯形,求点P坐标.

小题1:(1)判断点C是否为弧OB的中点?并说明理由;
小题2:(2)求B、C两点的坐标;
小题3:(3)求直线CD的函数解析式;
小题4:(4)点P在线段OB上,且满足四边形OPCD是等腰梯形,求点P坐标.
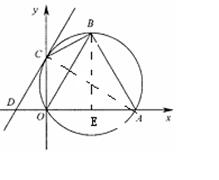
小题1:解:(1)C为弧OB的中点
联结AC
∵OC⊥OA ∴AC为圆的直径 --------------------------------------1分
∴∠ABC=90°
∵△OAB为等边三角形
∴∠ABO=∠AOB=∠BAO=60°
∵∠ACB=∠AOB=60°
∴∠COB=∠OBC=30°
∴弧OC=弧BC -----------------------2分
即C为弧OB的中点
小题2:(2)过点B作BE⊥OA于E
∵A(2,0) ∴OA=2
∴OE=1,BE=
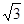
∴点B的坐标是(1,
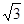 )
) ∵C为弧OB的中点,CD是圆的切线,AC为圆的直径
∴AC⊥CD,AC⊥OB ∴∠CAO=∠OCD=30°∴
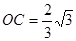
∴C(0,
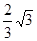 )
) 小题3:(3)在△COD中,∠ COD=90°,
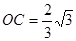
∴OD=
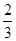 ∴D(-
∴D(-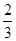 ,0)
,0) ∴直线CD的解析式为:
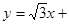
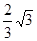
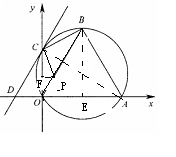
小题4:(4)∵四边形OPCD是等腰梯形
∴∠CDO=∠DCP=60°
∴∠OCP=∠COB =30°
∴PC="PO "
过点P 作PF⊥OC于F, 则OF=
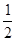 OC=
OC=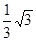 ,
,∴ PF=
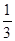
∴ 点P的坐标为:(
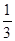 ,
,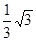 )
)略

练习册系列答案
相关题目
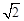 ,若在⊙O上找一点C,使AC=
,若在⊙O上找一点C,使AC=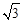 ,则∠BAC= ▲ °.
,则∠BAC= ▲ °. 的切线,切点分别是A、B,若∠APB=60°,PA=4.则⊙⊙的半径是__________.
的切线,切点分别是A、B,若∠APB=60°,PA=4.则⊙⊙的半径是__________.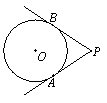

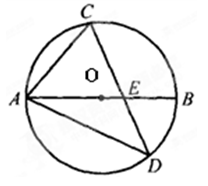
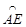 是劣弧
是劣弧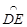 的2倍;⑤DE=DC。其中正确结论有( )
的2倍;⑤DE=DC。其中正确结论有( )