题目内容
【题目】如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A,O,分别与两坐标轴的正半轴交于点E,F.当EF⊥OA时,此时EF= . 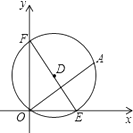
【答案】![]()
【解析】解:连接AE、OD,作AB⊥x轴于B,OA与EF垂直于C,如图1,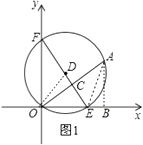
∵A(4,3),
∴OA= ![]() =5,
=5,
∵∠EOF=90°,
∴EF为⊙D的直径,
∵EF⊥OA,
∴CO=AC= ![]() OA=
OA= ![]() ,
,
∴EO=EA,
设OE=t,则AE=t,BE=4﹣t,
在Rt△ABE中,AB=3,
∵AB2+BE2=AE2 ,
∴32+(4﹣t)2=t2 , 解得t= ![]() ,
,
在Rt△OEC中,CE= ![]() =
= ![]() ,
,
在Rt△OCD中,设⊙D的半径为r,则OD=r,CD=r﹣ ![]() ,
,
∵DC2+OC2=OD2 ,
(r﹣ ![]() )2+(
)2+( ![]() )2=r2 , 解得r=
)2=r2 , 解得r= ![]() ,
,
∴EF=2r= ![]() ;
;
故答案为 ![]() .
.
作出辅助线,利用两点的距离公式计算出OA,根据圆周角定理得到EF为⊙D的直径,再根据垂径定理得到CO的值,设OE=t,根据勾股定理得出关于t的方程,进而计算出CE的值,设⊙D的半径为r,则OD=r,利用勾股定理得出关于t的方程,解出r的值即可.

练习册系列答案
相关题目