Question

【题目】二次函数y=ax2+bx+c（a＞0）的顶点为P，其图像与x轴有两个交点A（﹣m，0），B（1，0），交y轴于点C（0，﹣3am+6a），以下说法：
①m=3；
②当∠APB=120°时，a= ；
③当∠APB=120°时，抛物线上存在点M（M与P不重合），使得△ABM是顶角为120°的等腰三角形；
④抛物线上存在点N，当△ABN为直角三角形时，有a≥
正确的是（ ）
A.①②
B.③④
C.①②③
D.①②③④

Answer 1

【答案】D
【解析】解：①∵点A（﹣m，0）、B（1，0）在抛物线y=ax2+bx+c上，
∴ ，
由①﹣②得
am2﹣bm﹣a﹣b=0，
即（m+1）（am﹣a﹣b）=0．
∵A（﹣m，0）与B（1，0）不重合，
∴﹣m≠1即m+1≠0，
∴m= ，
∴点C的坐标为（0，3a﹣3b），
∵点C在抛物线y=ax2+bx+c上，
∴c=3a﹣3b，
代入②得a+b+3a﹣3b=0，即b=2a，
∴m= =3，故①正确；
②∵m=3，∵A（﹣3，0），
∴抛物线的解析式可设为y=a（x+3）（x﹣1），
则y=a（x2+2x﹣3）=a（x+1）2﹣4a，
∴顶点P的坐标为（﹣1，﹣4a）．
根据对称性可得PA=PB，
∴∠PAB=∠PBA=30°．
设抛物线的对称轴与x轴的交点为G，
则有PG⊥x轴，
∴PG=AGtan∠PAG=2× = ，
∴4a= ，
∴a= ，故②正确；
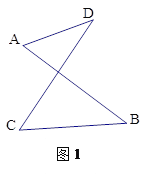
③在第一象限内作∠MBA=120°，且满足BM=BA，过点M作MH⊥x轴于H，如图1，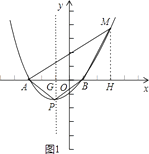

在Rt△MHB中，∠MBH=60°，
则有MH=4sin60°=4× =2 ，BH=4cos60°=4× =2，
∴点M的坐标为（3，2 ），
当x=3时，y= （3+3）（3﹣1）=2 ，
∴点M在抛物线上，故③正确；
④∵点N在抛物线上，∴∠ABN≠90°，∠BAN≠90°．
当△ABN为直角三角形时，∠ANB=90°，
此时点N在以AB为直径的⊙G上，
因而点N在⊙G与抛物线的交点处，
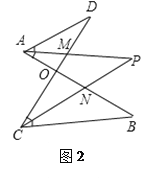
要使点N存在，点P必须在⊙G上或⊙G外，如图2，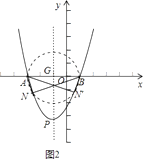

则有PG≥2，即4a≥2，也即a≥ ，故④正确．
故选D．
①把A、B两点的坐标分别代入抛物线的解析式得到①式和②式，将两式相减即可得到m= ，即可得到C（0，3a﹣3b），从而得到c=3a﹣3b，代入②式，就可解决问题；
②设抛物线的对称轴与x轴的交点为G，则有PG⊥x轴，只需求出点P的坐标就可解决问题；
③在第一象限内作∠MBA=120°，且满足BM=BA，过点M作MH⊥x轴于H，如图1，只需求出点M的坐标，然后验证点M是否在抛物线上，就可解决问题；
④易知点N在抛物线上且△ABN为直角三角形时，只能∠ANB=90°，此时点N在以AB为直径的⊙G上，因而点N在⊙G与抛物线的交点处，要使点N存在，点P必须在⊙G上或⊙G外，如图2，只需根据点与圆的位置关系就可解决问题．