题目内容
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为 . 
【答案】4或 ![]()
【解析】解:分两种情况:
①当∠DEC=90°时,△DCE为直角三角形,如图1,
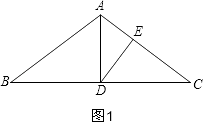
∴∠AED=90°,
∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠DAE=∠DAC,
∴△ADE∽△ACD,
∴∠ADC=∠AED=90°,
∴AD⊥BC,
∴BD= ![]() BC=
BC= ![]() ×8=4;
×8=4;
②当∠EDC=90°时,△DCE为直角三角形,如图2,

过A作AF⊥BC于F,则BF=4,
∵∠ADE+∠EDC=∠B+∠BAD,
∠ADE=∠B,
∴∠EDC=∠BAD=90°,
∴∠BAD=∠BFA=90°,
∵∠B=∠B,
∴△BFA∽△BAD,
∴ ![]() ,
,
∵AB=5,
∴ ![]() ,
,
∴BD= ![]() ,
,
综上所述,BD为4或 ![]() ,
,
所以答案是:4或 ![]() .
.
【考点精析】利用等腰三角形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通 过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛, 每位参赛学生听写![]() 个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数
个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数![]() 绘制成了以下不完整的统计图.
绘制成了以下不完整的统计图.

听写正确的汉字个数 | 组中值 |
|
|
|
|
|
|
|
|
根据以上信息回答下列问题:
(1)补全频数分布直方图;
(2)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
(3)该校共有![]() 名学生,如果听写正确的汉字个数不少于
名学生,如果听写正确的汉字个数不少于![]() 个定位良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.
个定位良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.