题目内容
【题目】如图,在等边△ABC中,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN、MN,
(1)求证:△CMN是等边三角形;
(2)判断CN与⊙O的位置关系,并说明理由;
(3)若AD:AB=3:4,BN=4,求等边△ABC的边长.
【答案】
(1)证明:△CMN是等边三角形,
理由:在△BCN与△ACM中, 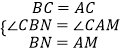 ,
,
∴△BCN≌△ACM,
∴CN=CM,∠BCN=∠ACM,
∴∠BCN﹣∠ACN=∠ACM﹣∠ACN,
即∠MCN=∠ACB=60°,
∴△CMN是等边三角形
(2)解:连接OA.OB.OC,

在△BOC与△AOC中,  ,
,
∴△BOC≌△AOC,
∴∠ACO=∠BCO= ![]() ACB=30°,
ACB=30°,
∵∠ACB=∠MCN=60°,
∴∠ACN=60°,
∴∠OCN=90°,
∴OC⊥CN,
∴CN是⊙O的切线
(3)解:∵∠ADB=∠ACB=60°,
∴∠ADB=∠ABC,
∵∠BAD=∠MAB,
∴△ABD∽△AMB,
∴ ![]() =
= ![]() ,
,
∵AM=BN=4,
∴AB=3.
∴等边△ABC的边长是3.
【解析】(1)利用边角边定理判定出三角形△BCN≌△ACM,再由三角形全等的性质得CN=CM,∠BCN=∠ACM,从而找到∠MCN=∠ACB=60°得到结论;(2)先由边边边得出△BOC≌△AOC,再由三角形全等的性质得∠ACO= 30°,由平角的定义得∠ACN=60°,进而∠OCN=90°得出CN是⊙O的切线;(3)由同弧所对的圆周角相等得∠ADB=∠ACB,进而得∠ADB=∠ABC从而△ABD∽△AMB,由相似三角形的性质得![]() =
= ![]() 得到AB的长度,最终得出等边△ABC的边长。
得到AB的长度,最终得出等边△ABC的边长。
【考点精析】关于本题考查的圆周角定理和直线与圆的三种位置关系,需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能得出正确答案.






