题目内容
【题目】探究:如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上的动点,且
上的动点,且![]() .
.
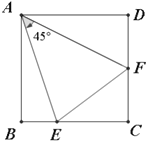
(1)如果将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() .请你画出图形(旋转后的辅助线).你能够得出关于
.请你画出图形(旋转后的辅助线).你能够得出关于![]() ,
,![]() ,
,![]() 的一个结论是________.
的一个结论是________.
(2)如果点![]() ,
,![]() 分别运动到
分别运动到![]() ,
,![]() 的延长线上,如图,请你能够得出关于
的延长线上,如图,请你能够得出关于![]() ,
,![]() ,
,![]() 的一个结论是________.
的一个结论是________.

(3)变式:如图,将题目改为“在四边形![]() 中,
中,![]() ,且
,且![]() ,点
,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上的动点,且
上的动点,且![]() ”,请你猜想关于
”,请你猜想关于![]() ,
,![]() ,
,![]() 有什么关系?并验证你的猜想.
有什么关系?并验证你的猜想.

【答案】(1)EF=BE+DF,画图如图所示;(2)BE= DF+EF;(3)EF=BE+DF,理由见解析
【解析】
(1)画出图形,证明△AEF≌△AEF′,得到EF=EF′,根据EF′=BE+BF′=BE+DF得到结果;
(2)将△ADF绕点A顺时针旋转90°,证明△AEF≌△AEF′,得到EF=EF′,从而可说明BE= DF+EF;
(3)将△ADF绕点A顺时针旋转,使AD与AB重合,证明∠ABF′+∠ABE=180°,说明F′、B、E三点共线,再证明△AEF≌△AEF′,得出EF=EF′,从而可说明EF=BE+DF.
解:(1)画图如图所示,旋转后点F的对应点为F′,AD与AB重合,
∵∠EAF=45°,
∴∠EAF′=∠EAF=45°,
在△AEF和△AEF′中,
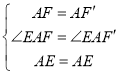 ,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又∵EF′=BE+BF′=BE+DF,
∴EF=BE+DF,
故答案为:EF=BE+DF;
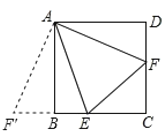
(2)将△ADF绕点A顺时针旋转90°,旋转后点F的对应点为F′,AD与AB重合,
∵∠EAF=45°,
∴∠F′AE=45°,AF=AF′,
在△AEF和△AEF′中,
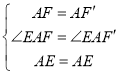 ,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
而DF=BF′,
∴BE=BF′+EF′=DF+EF,
故答案为:BE= DF+EF;
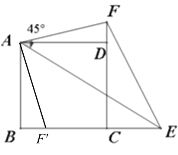
(3)EF=BE+DF,
理由是:如图,将△ADF绕点A顺时针旋转,使AD与AB重合,
则△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF=AF′,BF′=DF,∠ABF′=∠D,
又∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠EAF=∠DAF+∠BAE=∠BAE+∠BAF′,
∴∠EAF=∠EAF′,
又∵∠ABC+∠ADC=180°,
∴∠ABF′+∠ABE=180°,
∴F′、B、E三点共线,
在△AEF和△AEF′中,
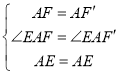 ,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又∵EF′=BE+BF′=BE+DF,
∴EF=BE+DF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案