题目内容
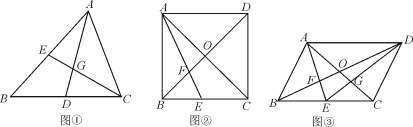
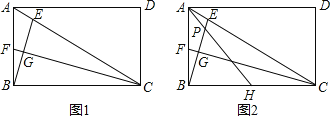
【题目】如图,在矩形ABCD中,点E是对角线AC上一动点,连接BE,作CF⊥BE分别交BE于点G,AB于点F.
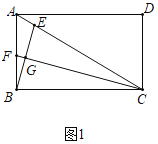
(1)如图1,若CF恰好平分∠BCA,求证:△CGE≌△CGB;
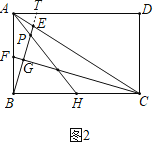
(2)如图2,若![]() =
=![]() ,取BC的中点H,连接AH交BE于点P,求证:
,取BC的中点H,连接AH交BE于点P,求证:
①AH=3AP;
②BH2=BFBA.
【答案】(1)见解析;(2)①见解析;②见解析
【解析】
(1)根据ASA证明三角形全等即可.
(2)①延长BE交AD于T.利用平行线分线段成比例定理解决问题即可.
②证明△ABT∽△BCF,推出![]() 可得结论.
可得结论.
解:证明:(1)如图1中,
∵CF平分∠ACB,
∴∠ECG=∠BCG,
∵CF⊥BE,
∴∠CGB=∠CGE=90°,
∵CG=CG,
∴△CGE≌△CGB(ASA).
(2)①如图2中,延长BE交AD于T.
∵![]() ,
,
∴![]() ,
,
∵四边形ABCD是矩形,
∴AT∥BC,
∴![]() ,
,
∵BH=BC,
∴![]() ,
,
∴![]() ,
,
∴AH=3AP.
②∵四边形ABCD是矩形,
∴∠CBF=∠BAT=90°,
∵CF⊥BE,
∴∠ABT+∠TBC=90°,∠TBC+∠BCF=90°,
∴∠ABT=∠BCF,
∴△ABT∽△BCF,
∴![]() ,
,
∵AT=![]() BC=
BC=![]() BH,BC=2BH,
BH,BC=2BH,
∴BFBA=ATBC=![]() BH2BH=BH2,
BH2BH=BH2,
∴BH2=BFBA.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目