Question

【题目】如图，在△ABC中，AB＝AC，点O为∠BAC的平分线上一点，连接OB、OC．

（1）求证：OB＝OC；

（2）若OA＝OC，∠BAC＝46°，求∠OCB的度数．

Answer 1

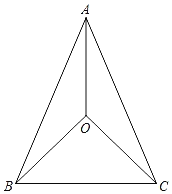
【答案】（1）见解析．（2）44°

【解析】

（1）由OA平分∠BAC可知∠BAO＝∠CAO，由SAS即可证明△BAO≌△CAO，从而得出结论．

（2）由（1）可知∠OAC＝∠OAB＝23°，由OA＝OC可知∠OAC＝∠OCA＝23°，由三角形外角性质可知∠COB＝2∠OAC+2∠OAB＝2∠BAC即可解答．

证明：（1）∵OA平分∠BAC，

∴∠BAO＝∠CAO＝∠BAC．

在△BAO和△CAO中，

∴△BAO≌△CAO（SAS）

∴OB＝OC．

（2）由（1）得∴∠BAO＝∠CAO＝∠BAC，OB＝OC，

∵OA＝OC，

∴OA＝OB＝OC，

∴∠OAC＝∠OCA＝∠BAO＝∠OBA＝23°，

∵∠COB＝∠OAC+∠OCA+∠BAO+∠OBA＝2∠BAC＝92°．

∴∠OCB＝（180°﹣92°）÷2＝44°