题目内容
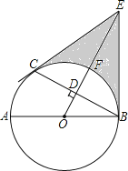
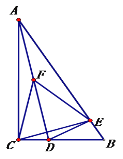
【题目】如图,△ABC中,已知∠C=90°,∠B=60°,点D在边BC上,过D作DE⊥AB于E.
(1)连接AD,取AD的中点F,连接CF,EF,判断△CEF的形状,并说明理由
(2)若BD=![]() CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
CD.把△BED绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
【答案】(1)等边三角形,见解析;(2)60°或135°
【解析】
(1)有直角三角形斜边的中线等于斜边的一半可得FC=FE,再证明∠CFE=60°即可;
(2)根据∠B=60°,∠DEB=90°,可知BD=![]() DE,又BD=
DE,又BD=![]() CD,则DC=DE,将△BED绕着点D逆时针旋转m°(0<n<180);分点B落在Rt△ABC的AB和AC上两种情况解答即可.
CD,则DC=DE,将△BED绕着点D逆时针旋转m°(0<n<180);分点B落在Rt△ABC的AB和AC上两种情况解答即可.
解:(1)△CEF为等边三角形,理由如下:
∵∠ACD=90°,∠B=60°,
∴∠CAB=30°
∵∠ACD=∠AED=90°,F是AD中点
∴CF=AF=DF=![]() AD, EF= AF=DF=
AD, EF= AF=DF=![]() AD
AD
∴CF=EF,∠CAF=∠FCA, ∠FAE=∠AEF,
∴∠CFD=∠CAF+∠FCA=2∠CAF, ∠EFD=∠EAF+∠AEF=2∠EAF,
∵∠CFE=∠CFD+∠EFD=2(∠CAF+∠EAF)=2∠CAB=60°
∴△CEF为等边三角形;
(2)①若点B落在AB边上的点M时,
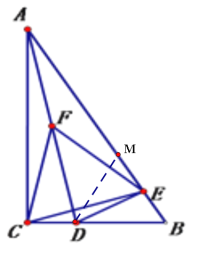
∵DB=DM, ∠B=60°
∴△DBM为等边三角形,m=∠BDM=60°
②若点B落在AC边上的点N时,
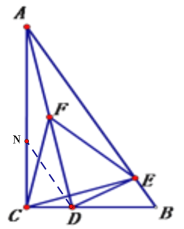
∵DB=DN=![]() CD, ∠C=90°
CD, ∠C=90°
∴△DBN为等腰直角三角形,
m=∠BDM=135°
综上所述,点B落在三角形的边上时,m=60°或135°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目