题目内容
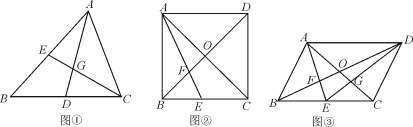
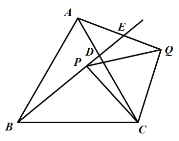
【题目】如图,在边长为 6 的等边△ABC 中,D 为 AC 上一点,AD=2,P 为 BD 上一点,连接 CP,以 CP 为 边,在 PC 的右侧作等边△CPQ,连接 AQ 交 BD 延长线于 E,当△CPQ 面积最小时,QE=____________.
【答案】![]()
【解析】
如图,过点D作DF⊥BC于F,由“SAS”可证△ACQ≌△BCP,可得AQ=BP,∠CAQ=∠CBP,由直角三角形的性质和勾股定理可求BD的长,由锐角三角函数可求BP的长,由相似三角形的性质可求AE的长,即可求解.
如图,过点D作DF⊥BC于F,
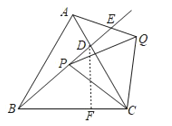
∵△ABC,△PQC是等边三角形,
∴BC=AC,PC=CQ,∠BCA=∠PCQ=60°,
∴∠BCP=∠ACQ,且AC=BC,CQ=PC,
∴△ACQ≌△BCP(SAS)
∴AQ=BP,∠CAQ=∠CBP,
∵AC=6,AD=2,
∴CD=4,
∵∠ACB=60°,DF⊥BC,
∴∠CDF=30°,
∴CF=![]() CD=2,DF=CF÷tan30°=
CD=2,DF=CF÷tan30°=![]() CF=2
CF=2![]() ,
,
∴BF=4,
∴BD=![]() =
=![]() =2
=2![]() ,
,
∵△CPQ是等边三角形,
∴S△CPQ=![]() CP2,
CP2,
∴当CP⊥BD时,△CPQ面积最小,
∴cos∠CBD=![]() ,
,
∴![]() ,
,
∴BP=![]() ,
,
∴AQ=BP=![]() ,
,
∵∠CAQ=∠CBP,∠ADE=∠BDC,
∴△ADE∽△BDC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴QE=AQAE=![]()
故答案为;![]() .
.

练习册系列答案
相关题目