题目内容
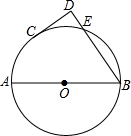
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2
.若将⊙P向上平移,则⊙P与x轴相切时点P坐标为( )

| 3 |
| A.(3,2) | B.(3,3) | C.(3,4) | D.(3,5) |

当P移到P′点时,⊙P与x轴相切,
过P作直径MN⊥AB与D,连接AP,
由垂径定理得:AD=BD=
| 1 |
| 2 |
| 3 |
∵DP=|-1|=1,
由勾股定理得:AP=
| AD2+PD2 |
∴PP′=2+1=3,
∵P(3,-1),
∴P′的坐标是(3,2),
故选A.


练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目




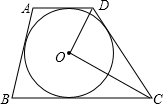
 长线于点F.已知BC=8,DE=2.
长线于点F.已知BC=8,DE=2.