题目内容
在平面直角坐标系中，作以原点O为圆心，半径为4的⊙O，试确定点A（-2，-3），B（4，-2），C（-2
，2）与⊙O的位置关系．
| 3 |
连接OA、OB、OC，
∵A（-2，-3），
∴由勾股定理得：OA=
=
＜4，
即A与⊙O的位置关系是A在⊙O内；
∵B（4，-2），
∴由勾股定理得：OB=
=
＞4，
即B与⊙O的位置关系是B在⊙O外；
∵C（-2
，2），
∴由勾股定理得：OC=
=4=4，
即C与⊙O的位置关系是C在⊙O上．
∵A（-2，-3），
∴由勾股定理得：OA=
| 22+32 |
| 13 |
即A与⊙O的位置关系是A在⊙O内；
∵B（4，-2），
∴由勾股定理得：OB=
| 42+22 |
| 20 |
即B与⊙O的位置关系是B在⊙O外；
∵C（-2
| 3 |
∴由勾股定理得：OC=
(2
|
即C与⊙O的位置关系是C在⊙O上．
练习册系列答案
相关题目
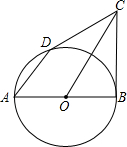
点D，E为CH的中点，连接AE并延长交BD于F，直线CF交直线AB于点G．
