题目内容
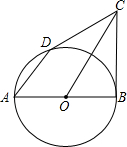
如图.已知AB是⊙O的直径.C是⊙O上一点,直线CE与AB的延长线相交于点E,AD⊥CE于点D,AD交⊙O于点F.AC平分∠DAE.
(1)求证:CE是⊙O的切线.
(2)若DC+DF=6.⊙O的直径为10,求AF的长.

(1)求证:CE是⊙O的切线.
(2)若DC+DF=6.⊙O的直径为10,求AF的长.

(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠CAO,
∵OA=OC,
∴∠OCA=∠CAO,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥DE,
∴OC⊥DE,
∵OC为半径,
CE是⊙O的切线;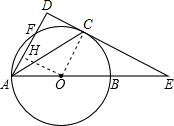
(2)设DC=x.则DF=6-x,过O作OH⊥AD于H,
∵AD⊥DE,OC⊥DE,
∴∠OHD=∠D=∠OCD=90°,
∴四边形OHDC是矩形,
∴DH=OC=5,FH=5-(6-x)=x-1,
∵OH⊥AF,
∴AH=FH=x-1,
在Rt△AOH中,AO2=AH2+HO2,
∴52=(x-1)2+x2,
x=4,x=-3(不符合题意舍去),
∴AF=2FH=2(4-1)=6.
∵AC平分∠DAB,
∴∠DAC=∠CAO,
∵OA=OC,
∴∠OCA=∠CAO,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥DE,
∴OC⊥DE,
∵OC为半径,
CE是⊙O的切线;

(2)设DC=x.则DF=6-x,过O作OH⊥AD于H,
∵AD⊥DE,OC⊥DE,
∴∠OHD=∠D=∠OCD=90°,
∴四边形OHDC是矩形,
∴DH=OC=5,FH=5-(6-x)=x-1,
∵OH⊥AF,
∴AH=FH=x-1,
在Rt△AOH中,AO2=AH2+HO2,
∴52=(x-1)2+x2,
x=4,x=-3(不符合题意舍去),
∴AF=2FH=2(4-1)=6.

练习册系列答案
相关题目





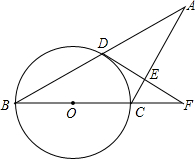 交BC的延长线于点F.
交BC的延长线于点F.