题目内容
在?ABCD中，AB=10，∠ABC=60°，以AB为直径作⊙O，边CD切⊙O于点E．
（1）圆心O到CD的距离是______．
（2）求由弧AE、线段AD、DE所围成的阴影部分的面积．（结果保留π和根号）
（1）圆心O到CD的距离是______．
（2）求由弧AE、线段AD、DE所围成的阴影部分的面积．（结果保留π和根号）
（1）连接OE．
∵边CD切⊙O于点E．
∴OE⊥CD
则OE就是圆心O到CD的距离，则圆心O到CD的距离是
×AB=5．
故答案是：5；
（2）∵四边形ABCD是平行四边形．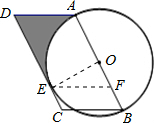
∴∠C=∠DAB=180°-∠ABC=120°，
∴∠BOE=360°-90°-60°-120°=90°，
∴∠AOE=90°，
作EF∥CB，∴∠OFE=∠ABC=60°，
在直角三角形OEF中，OE=5，
∴OF=OE•tan30°=
．EC=BF=5-
．
则DE=10-5+
=5+
，
则直角梯形OADE的面积是：
（OA+DE）×OE=
（5+5+
）×5=25+
．
扇形OAE的面积是：
=
．
则阴影部分的面积是：25+
-
．
∵边CD切⊙O于点E．
∴OE⊥CD
则OE就是圆心O到CD的距离，则圆心O到CD的距离是
| 1 |
| 2 |
故答案是：5；
（2）∵四边形ABCD是平行四边形．
∴∠C=∠DAB=180°-∠ABC=120°，
∴∠BOE=360°-90°-60°-120°=90°，
∴∠AOE=90°，
作EF∥CB，∴∠OFE=∠ABC=60°，
在直角三角形OEF中，OE=5，
∴OF=OE•tan30°=
5
| ||
| 3 |
5
| ||
| 3 |
则DE=10-5+
5
| ||
| 3 |
5
| ||
| 3 |
则直角梯形OADE的面积是：
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 3 |
25
| ||
| 6 |
扇形OAE的面积是：
| 90π×52 |
| 360 |
| 25π |
| 4 |
则阴影部分的面积是：25+
25
| ||
| 6 |
| 25π |
| 4 |
练习册系列答案
阅读快车系列答案
相关题目
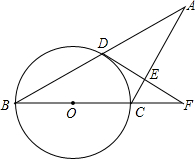交BC的延长线于点F．
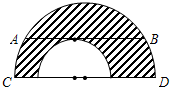
点D，E为CH的中点，连接AE并延长交BD于F，直线CF交直线AB于点G．
