题目内容
【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足![]() .
.
(1)求A,B的坐标.
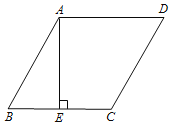
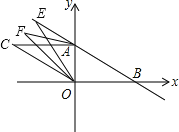
(2)如图1, E为第二象限内直线AB上的一点,且满足![]() ,求点E的横坐标.
,求点E的横坐标.
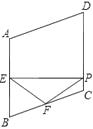
(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

【答案】(1)A(0,3),B(4,0);(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据非负数的性质列式求出m、n的值,然后写出点A、B的坐标即可;
(2)设点E的横坐标为a,然后利用三角形的面积列式求出a的值,再利用待定系数法求出直线AB的解析式,然后求解即可;
(3)根据平移的性质可得AB∥OC,AC∥OB,根据平行线的性质可得∠OEB=∠COE,∠CAE=∠ABO,然后根据角平分线的定义可得![]() ,
,![]() ,再根据三角形的内角和定理列式整理即可得解.
,再根据三角形的内角和定理列式整理即可得解.
解:(1)由非负数的性质得,m-3=0,n-4=0,
解得m=3,n=4,
所以,A(0,3)B(4,0);
(2)设点E的横坐标为a,
![]() ,
,
![]() ,
,
解得a=![]() ,
,
设直线AB的解析式为y=kx+b,
则![]()
解得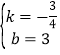
所以,直线AB的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
所以,点E的坐标为![]() ;
;
(3)由平移的性质,AB∥OC,AC∥OB,
∴∠OEB=∠COE,∠CAE=∠ABO,
∵OF平分∠COE,AF平分∠EAC,
![]() ,
,
由三角形的内角和定理,∠OEB+∠EAF=∠F+∠EOF,
![]() ,
,
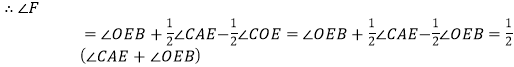 ,
,
∵∠ABO+∠OEB=α,
![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目