题目内容
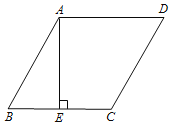
【题目】如图,菱形ABCD中,AE⊥BC于点E,∠BAE=30°,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.
【答案】⑴菱形各角的度数为60°、120°、60°、120°;⑵AE的长为![]() cm
cm
【解析】
(1)由AE⊥BC,得∠AEB=90°,根据三角形的内角和即可求出∠B=60°,
根据菱形的对角相等,邻角互补即可求解.
(2)根据菱形的四条边相等得到AB=AD=4,因为∠BAE=30°,所以BE=2cm,利用勾股定理即可求出AE的长.
⑴ ∵AE⊥BC
∴∠AEB=90°
∵∠BAE=30°
∴∠B=60°
∵菱形ABCD
∴∠D=∠B=60°,AB∥CD
∴∠BAD=∠C=120°
答:菱形各角的度数为60°、120°、60°、120°
⑵ ∵菱形ABCD
∴AB=AD=4
∵∠BAE=30°
∴BE=2
∴AE=![]()
答:AE的长为![]() cm
cm

练习册系列答案
相关题目