جâؤ؟ؤعبف
،¾جâؤ؟،؟بçح¼£¨1£©£¬AD£¬BC½»سعOµم£¬¸ù¾ف،°ب½اذخؤع½ا؛حتا180،م،±£¬²»ؤرµأ³ِء½¸ِب½اذخضذµؤ½ا´وشعزشدآ¹طدµ£؛¢ظ،دDOC£½،دAOB£»¢ع،دD+،دC£½،دA+،دB£®
£¨جل³ِختج⣩
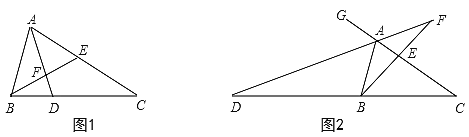
·ض±ً×÷³ِ،دBAD؛ح،دBCDµؤئ½·ضدك£¬ء½جُ½ائ½·ضدك½»سعµمE£¬بçح¼£¨2£©£¬،دEسë،دD،¢،دBض®¼نتا·ٌ´وشعؤ³ضضتء؟¹طدµؤط£؟
£¨½â¾ِختج⣩
خھءث½â¾ِةدأوµؤختج⣬خزأادب´س¼¸¸ِجطتâاé؟ِ؟ھت¼ج½¾؟£®
زرضھ،دBADµؤئ½·ضدكسë،دBCDµؤئ½·ضدك½»سعµمE£®
£¨1£©بçح¼£¨3£©£¬بôAB،خCD£¬،دD£½30،م£¬،دB£½40،م£¬شٍ،دE£½،، ،،£®
£¨2£©بçح¼£¨4£©£¬بôAB²»ئ½ذذCD£¬،دD£½30،م£¬،دB£½50،م£¬شٍ،دEµؤ¶بتتا¶àةظؤط£؟
ذ،أ÷تاصâرùث¼؟¼µؤ£¬اëؤم°ïثûحê³ةحئہي¹³ج£؛
ز×ض¤،دD+،د1£½،دE+،د3£¬،دB+،د4£½،دE+،د2£¬
،à،دD+،د1+،دB+،د4£½،، ،،£¬
،كCE،¢AE·ض±ًتا،دBCD،¢،دBADµؤئ½·ضدك£¬
،à،د1£½،د2£¬،د3£½،د4£®
،à2،دE£½،، ،،£¬
سض،ك،دD£½30،م£¬،دB£½50،م£¬
،à،دE£½،، ،،¶ب£®
£¨3£©شع×ـ½لا°ء½ختµؤ»ù´،ةد£¬½èضْح¼£¨2£©£¬ض±½سذ´³ِ،دEسë،دD،¢،دBض®¼نµؤتء؟¹طدµتا£؛،، ،،£®
£¨ہà±بس¦سأ£©
بçح¼£¨5£©£¬،دBADµؤئ½·ضدكAEسë،دBCDµؤئ½·ضدكCE½»سعµمE£®
زرضھ£؛،دD£½m،م،¢،دB£½n،م£¬£¨m£¼n£©اَ£؛،دEµؤ¶بت£®

،¾´ً°¸،؟،¾½â¾ِختجâ،؟£¨1£©35،م£»£¨2£©2،دE+،د3+،د2£¬،دD+،دB£¬40،م£»£¨3£©،دE£½![]() £»،¾ہà±بس¦سأ،؟،دE£½
£»،¾ہà±بس¦سأ،؟،دE£½![]() £¨n©پm£©،م£®
£¨n©پm£©،م£®
،¾½âخِ،؟
½â¾ِختجâ£؛£¨1£©¸ù¾فء½¸ِب½اذخµؤسذز»¶ش¶ش¶¥½ادàµبµأ£؛،دD+،دDCE£½،دE+،دDAE£¬،دE+،دECB£½،دB+،دEAB£¬ء½ت½دà¼س؛َ£¬شظ¸ù¾ف½ائ½·ضدكµؤ¶¨زه؟ةµأ½لآغ£»
£¨2£©ح¬ہيءذء½ت½دà¼س؟ةµأ½لآغ£»
£¨3£©¸ù¾ف£¨1£©؛ح£¨2£©؟ةµأ½لآغ£»
ہà±بس¦سأ£؛ت×دبرس³¤BC½»ADسعµمF£¬سةب½اذخحâ½اµؤذشضت£¬؟ةµأ،دBCD£½،دB+،دBAD+،دD£¬سضسة½ائ½·ضدكµؤذشضت£¬¼´؟ةاَµأ´ً°¸£®
½â¾ِختجâ£؛£¨1£©بçح¼3£¬،ك،دD+،دDCE£½،دE+،دDAE£¬
،دE+،دECB£½،دB+،دEAB£¬
،à،دD+،دDCE+،دB+،دEAB£½2،دE+،دDAE+،دECB£¬
،كECئ½·ض،دECB£¬AEئ½·ض،دBAD£¬
،à،دDCE£½،دECB£¬،دDAE£½،دBAE£¬
،à2،دE£½،دB+،دD£¬
،à،دE£½![]()
،à،دE£½![]() £¨30،م+40،م£©£½
£¨30،م+40،م£©£½![]() ،ء70،م£½35،م£»
،ء70،م£½35،م£»
¹ت´ً°¸خھ£؛35،م£»
£¨2£©بçح¼£¨4£©£¬،دD+،د1£½،دE+،د3£¬،دB+،د4£½،دE+،د2£¬
،à،دD+،د1+،دB+،د4£½2،دE+،د3+،د2£¬
،كCE،¢AE·ض±ًتا،دBCD،¢،دBADµؤئ½·ضدك£¬
،à،د1£½،د2£¬،د3£½،د4£®
،à2،دE£½،دD+،دB£¬
،à،دE£½![]() £¬
£¬
سض،ك،دD£½30،م£¬،دB£½50،م£¬
،à،دE£½40¶ب£®
¹ت´ً°¸خھ£؛2،دE+،د3+،د2£¬،دD+،دB£¬40،م£»
£¨3£©سة£¨1£©؛ح£¨2£©µأ£؛،دE£½![]() £¬
£¬
¹ت´ً°¸خھ£؛،دE£½![]() £»
£»
ہà±بس¦سأ:
بçح¼£¨5£©£¬رس³¤BC½»ADسعF£¬
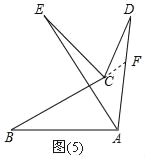
،ك،دBFD£½،دB+،دBAD£¬
،à،دBCD£½،دBFD+،دD£½،دB+،دBAD+،دD£¬
،كCEئ½·ض،دBCD£¬AEئ½·ض،دBAD
،à،دECD£½،دECB£½![]() ،دBCD£¬،دEAD£½،دEAB£½
،دBCD£¬،دEAD£½،دEAB£½![]() ،دBAD£¬
،دBAD£¬
،ك،دE+،دECB£½،دB+،دEAB£¬
،à،دE£½،دB+،دEAB©پ،دECB£½،دB+،دBAE©پ![]() ،دBCD£½،دB+،دBAE©پ
،دBCD£½،دB+،دBAE©پ![]() £¨،دB+،دBAD+،دD£©£½
£¨،دB+،دBAD+،دD£©£½![]() £¨،دB©پ،دD£©£¬
£¨،دB©پ،دD£©£¬
،ك،دD£½m،م،¢،دB£½n،م£¬
¼´،دE£½![]() £¨n©پm£©،م£®
£¨n©پm£©،م£®

 شؤ¶ء؟ى³µدµءذ´ً°¸
شؤ¶ء؟ى³µدµءذ´ً°¸،¾جâؤ؟،؟جهسخؤ»¯سأئ·ةجµê¹؛½ّہ؛اٍ؛حإإاٍ¹²20¸ِ£¬½ّ¼غ؛حتغ¼غبçدآ±ي£¬ب«²؟دْتغحê؛َ¹²»ٌہûبَ260شھ£®
ہ؛اٍ | إإاٍ | |
½ّ¼غ£¨شھ/¸ِ£© | 80 | 50 |
تغ¼غ£¨شھ/¸ِ£© | 95 | 60 |
اَ£؛£¨1£©¹؛½ّہ؛اٍ؛حإإاٍ¸÷¶àةظ¸ِ£؟
£¨2£©دْتغ6¸ِإإاٍµؤہûبَسëدْتغ¼¸¸ِہ؛اٍµؤہûبَدàµب£؟