题目内容
【题目】已知四边形ABCD为菱形，其边长为6，
，点P在菱形的边AD、CD及对角线AC上运动，当
时，则DP的长为________.
【答案】2或
或
【解析】
分以下三种情况求解：（1）点P在CD上，如图①，根据菱形的边长以及CP1=2DP1可得出结果；（2）点P在对角线AC上，如图②，在三角形CDP2中，可得出∠P2DC=90°，进而可得出DP2的长；（3）当点P在边AD上，如图③，过点D作
于点F，过点
作
于点E，设
，则
，再用含x的代数式表示出CE，EP3，CP3的长，根据勾股定理列方程求解即可.
解：（1）当点P在CD上时，如解图①，
，
，
；
（2）当点P在对角线AC上时，如解图②，
，
.
当
时，
，
；
图① 图②
（3）当点P在边AD上时，如解图③，过点D作于点F，过点作于点E，设，则，
，
，
，
，
，
，
.
，在
中，由勾股定理得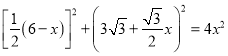
，解得
，
（舍）.
综上所述，DP的长为2或或.
故答案为：2或或.
练习册系列答案
相关题目
【题目】在直角坐标系中，我们把横、纵坐标都为整数的点叫做整点，设坐标轴的单位长度为1cm， 整点P从原点0出发，速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s) | 可以得到整点P的坐标 | 可以得到整点P的个数 |
1 | (0，1)（1，0） | 2 |
2 | (0，2)（1，1）(2,0) | 3 |
3 | (0,3)(1,2)(2,1)(3,0) | 4 |
. | · | . |
根据上表中的规律，回答下列问题:
（1）当整点P从点0出发4s时，可以得到的整点的个数为______个.
（2）当整点P从点O出发8s时，在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
（3）当整点P从点0出发______s时，可以得到整点(16,4)的位置.
