题目内容
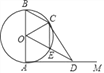
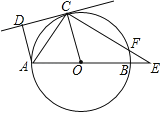
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上的一点,CE交⊙O于点F,连接OC,AC,若∠DAO=105°,∠E=30°.
(Ⅰ)求∠OCE的度数;
(Ⅱ)若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
【答案】(Ⅰ)45°;(Ⅱ)2![]() ﹣2.
﹣2.
【解析】分析:
(1)由CD是⊙O的切线可得OC⊥CD,结合AD⊥CD于点D可得OC∥AD,从而可得∠COE=∠DAE=105°,结合∠E=30°即可得到∠OCE=45°;
(2)如下图,过点O作OM⊥CF于点M,则CM=MF结合∠OCE=45°,OC=![]() 即可得到OM=CM=2=MF,结合∠E=30°可得OE=2OM=4,则由勾股定理可得ME=
即可得到OM=CM=2=MF,结合∠E=30°可得OE=2OM=4,则由勾股定理可得ME=![]() ,从而可得EF=ME-MF=
,从而可得EF=ME-MF=![]() .
.
详解:
(Ⅰ)∵CD是⊙O的切线,
∴OC⊥CD,又AD⊥CD,
∴AD∥OC,
∴∠COE=∠DAO=105°,
又∵∠E=30°,
∴∠OCE=180°﹣∠COE﹣∠E=45°;
(Ⅱ)如下图,过点O作OM⊥CE于M,
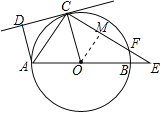
∴ CM=MF,∠OMC=∠OME=90°,
∵∠OCE=45°,
∴OM=CM=2=MF,
∵∠E=30°,
∴在Rt△OME中,OE=2OM=4,
∴ME=![]() ,
,
∴EF=ME-MF=![]() .
.

练习册系列答案
相关题目