题目内容
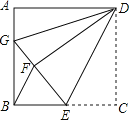
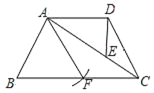
【题目】如图,已知梯形ABCD中,AD∥BC,AB=CD,点E在对角线AC上,且满足∠ADE=∠BAC.
(1)求证:CDAE=DEBC;
(2)以点A为圆心,AB长为半径画弧交边BC于点F,联结AF.求证:AF2=CECA.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据相似三角形的判定得出△ADE∽△CAB,再利用相似三角形的性质证明即可;
(2)根据相似三角形的判定得出△CDE∽△CAD,再利用相似三角形的性质证明即可.
试题解析:
证明(1)∵AD∥BC,
∴∠DAE=∠ACB,
∵∠ADE=∠BAC,
∴△ADE∽△CAB,
∴![]() ,
,
∴ABAE=DEBC,
∵AB=CD,
∴CDAE=DEBC;
(2)∵AD∥BC,AB=CD,
∴∠ADC=∠DAB,
∵∠ADE=∠BAC,
又∵∠ADC=∠ADE+∠CDE,∠DAB=∠BAC+∠CAD,
∴∠CDE=∠CAD,
∴△CDE∽△CAD,
∴![]() ,
,
∴CD2=CECA,
由题意,得AB=AF,AB=CD,
∴AF=CD,
∴AF2=CECA.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目