题目内容
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
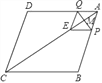
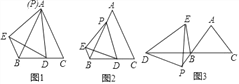
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
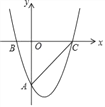
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
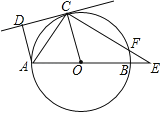
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)
【答案】(1)5;(2)4;(3)BD﹣BE =2acos55°.
【解析】试题分析:(1)先判断出∠BPE=∠CAD,进而判断出△PBE≌△ACD,即可得出BD+BE=BC=5;
(2)先构造出等边三角形,再判断出∠BPE=∠FPD,进而判断出△PBE≌△PFD,即可得出BD+BE=BF=4;
(3)类似于(2)的方法判断出△PBE≌△PFD得出BE=DF,再判断出BF=2BG,利用用锐角三角函数求出BG=acos55°,即可BD-BE=BF=2acos55°.
试题解析:解:(1)∵△ABC和△PDE是等边三角形,
∴PE=PD,AB=AC,∠DPE=∠CAB=60°,
∴∠BPE=∠CAD,
∴△PBE≌△ACD,
∴BE=CD,
∴BD+BE=BD+CD=BC=5,
故答案为5;
(2)如图2,过点P作PF∥AC交BC于F,
∴△FPB是等边三角形,
∴BF=PF=PB=AB﹣AP=4,∠BPF=60°,
∵△PDE是等边三角形,
∴PD=PE,∠DPE=60°,
∴∠BPE=∠FPD,
∴△PBE≌△PFD,
∴BE=DF,
∴BD+BE=BD+DF=BF=4;
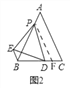
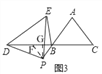
(3)如图3,
过点P作PF∥AC交BC于F,
∴∠BPF=∠BAC=70°,∠PFB=∠C,
∵AB=AC,∠BAC=70°,
∴∠ABC=∠C=55°,
∴∠PFB=∠C=∠PBF=55°,
∴PF=PB=a,
∵∠BPF=∠DPE=70°,
∴∠DPF=∠EPB,
∵PD=PE,
∴△PBE≌△PFD,
∴BE=DF,
过点P作PG⊥BC于G,
∴BF=2BG,
在Rt△BPG中,∠PBD=55°,
∴BG=BPcos∠PBD=acos55°,
∴BF=2BG=2acos55°,
∴BD﹣BE=BD﹣DF=BF=2acos55°.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】“发展脐橙产业,加快脱贫的步伐”.某脐橙种植户新鮮采摘了20筐脐橙,以每筐25千克为标准重量,超过或不足干克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:干克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)与标准重量比较,20筐脐橙总计超过或不足多少千克?
(2)若脐橙毎干克售价6.5元,则出售这20筐脐橙可获得多少元?