题目内容
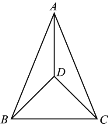
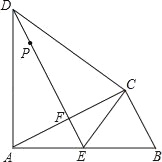
【题目】如图,△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,与AB相交于点E,连接CE.
(1)说明:AE=CE=BE;
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.
【答案】(1)证明见解析;(2)当点P在E处时,PB+PC=15cm.
【解析】
(1)根据等边三角形“三合一”的性质证得DE垂直平分AC;然后由等腰三角形的判定知AE=CE,根据等边对等角、直角三角形的两个锐角互余的性质以及等量代换求得∠BCE=∠B;最后根据等角对等边证得CE=BE,所以AE=CE=BE;
(2)由(1)知,DE垂直平分AC,故PC=PA;由等量代换知PB+PC=PB+PA;根据两点之间线段最短可知,当点P、B、A在同一直线上最小,所以点P在E处时最小.
(1)在等边三角形ADC中,∵DF⊥AC,∴DF垂直平分AC,∴AE=CE,∴∠ACE=∠CAE(等边对等角);
∵∠ACB=90°(已知),∴∠ACE+∠BCE=∠CAE+∠B=90°,∴∠BCE=∠B,∴CE=BE(等角对等边),∴AE=CE=BE;
(2)由(1)知,DE垂直平分AC,∴PC=PA,∴PB+PC=PB+PA;
∴当PB+PC最小时,也就是PB+PA最小,即点P、B、A在同一直线上最小,所以点P在E处时最小.
当点P在E处时,PB+PC=EB+EC=EB+EA=AB=15cm.

练习册系列答案
相关题目