题目内容
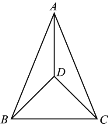
【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
【答案】(1)证明见解析;(2)∠ADB=135°.
【解析】
(1)根据∠BDC=90°,∠DBC=45°可推出DBDC,进而可证△ABD≌△ACD,即可证得∠BAD=∠CAD;(2)根据△ABD≌△ACD,可得∠ADB=∠ADC,又根据∠BDC=90°,∠ADB+∠ADC+∠BDC=360°,即可求出∠ADB的大小.
(1)∵∠BDC=90°,∠DBC=45°,
∴∠DCB=∠DBC=45°.
∴DB=DC.
在△ABD和△ACD中
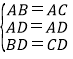 ,,
,,
∴△ABD≌△ACD.
∴∠BAD=∠CAD.
(2)∵△ABD≌△ACD,
∴∠ADB=∠ADC.
∵∠BDC=90°,
∴∠ADB=135°.

练习册系列答案
相关题目