题目内容
如图，E、F是边长为4的正方形ABCD边AD、CD上的动点，若AE=EF，EF⊥FM交BC于M，则△FMC的周长为______．
作AH⊥FM，设∠EAF=α，
∴∠AHF=∠AHM=90°
∵四边形ABCD是正方形，
∴AD=AB=BC=CD=4，∠D=∠B=90°
∵EF⊥FM，
∴∠EFM=90°
∵AE=AF，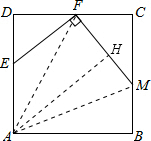
∴∠EAF=∠EFA=a，
∴∠AFH=90°-α=∠AFD，
在△ADF和△AHF中
，
∴△AFH≌△AFD﹙AAS﹚
∴DF=HF，AD=AH=4=AB；
在Rt△AHM和Rt△ABM中
∴Rt△AMH≌Rt△AMB，
∴HM=BM．
∵△FMC的周长=CF+FM+MC，
∴△FMC的周长=CF+FD+MB+MC=CD+CB=8．
故答案为：8．
∴∠AHF=∠AHM=90°
∵四边形ABCD是正方形，
∴AD=AB=BC=CD=4，∠D=∠B=90°
∵EF⊥FM，
∴∠EFM=90°
∵AE=AF，
∴∠EAF=∠EFA=a，
∴∠AFH=90°-α=∠AFD，
在△ADF和△AHF中
|
∴△AFH≌△AFD﹙AAS﹚
∴DF=HF，AD=AH=4=AB；
在Rt△AHM和Rt△ABM中
|
∴Rt△AMH≌Rt△AMB，
∴HM=BM．
∵△FMC的周长=CF+FM+MC，
∴△FMC的周长=CF+FD+MB+MC=CD+CB=8．
故答案为：8．
练习册系列答案
特高级教师点拨系列答案
相关题目
90°，得到△AFD．
