题目内容
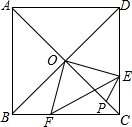
如图，正方形ABCD中，E是AD上一点（E与A、D不重合）．连接CE，将△CED绕点D顺时针旋转
90°，得到△AFD．
（1）猜想CE和AF之间的关系，并进行证明．
（2）连接EF，若∠ECD=30°，求∠AFE的度数．
90°，得到△AFD．（1）猜想CE和AF之间的关系，并进行证明．
（2）连接EF，若∠ECD=30°，求∠AFE的度数．
（1）CE=AF，且CE⊥AF．
证明：如图，∵△AFD是由△CED绕点D顺时针旋转90°而得到的．
∴△ADF≌△CDE，
∴CE=AF，∠1=∠2，DE=DF．
延长CE交AF于点G．
∵四边形ABCD是正方形，∠CDA=90°．
又∠3=∠4，∠2+∠4+∠EGA=∠1+∠3+∠CDE=180°
∴∠EGA=∠CDE=90°
即CE⊥AF；
（2）∵∠1=30°，∠2=30°又∠ADF=90°，
∴∠AFD=60°，
∵DE=DF，
∴∠EFD=45°，
∴∠AFE=∠AFD-∠EFD=15°．
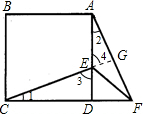
证明：如图，∵△AFD是由△CED绕点D顺时针旋转90°而得到的．
∴△ADF≌△CDE，
∴CE=AF，∠1=∠2，DE=DF．
延长CE交AF于点G．
∵四边形ABCD是正方形，∠CDA=90°．
又∠3=∠4，∠2+∠4+∠EGA=∠1+∠3+∠CDE=180°
∴∠EGA=∠CDE=90°
即CE⊥AF；
（2）∵∠1=30°，∠2=30°又∠ADF=90°，
∴∠AFD=60°，
∵DE=DF，
∴∠EFD=45°，
∴∠AFE=∠AFD-∠EFD=15°．
练习册系列答案
名校课堂系列答案
相关题目
