ĢāÄæÄŚČŻ
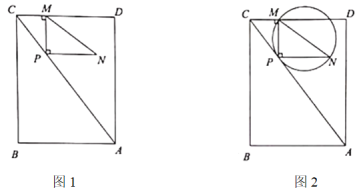
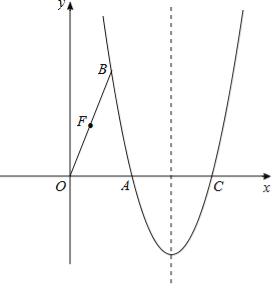
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]() ¾¹żµćA£Ø
¾¹żµćA£Ø![]() £¬0£©ŗĶµćB£Ø1£¬
£¬0£©ŗĶµćB£Ø1£¬![]() £©£¬ÓėxÖįµÄĮķŅ»øö½»µćĪŖC£®
£©£¬ÓėxÖįµÄĮķŅ»øö½»µćĪŖC£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©µćDŌŚ¶Ō³ĘÖįµÄÓŅ²ą£¬xÖįÉĻ·½µÄÅ×ĪļĻßÉĻ£¬ĒŅ”ĻBDA=”ĻDAC£¬ĒóµćDµÄ×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½ÓBD£¬½»Å×ĪļĻ߶Ō³ĘÖįÓŚµćE£¬Į¬½ÓAE£®
¢ŁÅŠ¶ĻĖıߊĪOAEBµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
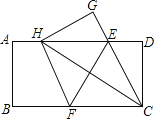
¢ŚµćFŹĒOBµÄÖŠµć£¬µćMŹĒÖ±ĻßBDµÄŅ»øö¶Æµć£¬ĒŅµćMÓėµćB²»ÖŲŗĻ£¬µ±”ĻBMF=![]() ”ĻMFOŹ±£¬ĒėÖ±½ÓŠ“³öĻ߶ĪBMµÄ³¤£®
”ĻMFOŹ±£¬ĒėÖ±½ÓŠ“³öĻ߶ĪBMµÄ³¤£®
”¾“š°ø”æ£Ø1£©![]() £®£Ø2£©D£Ø4£¬
£®£Ø2£©D£Ø4£¬![]() £©£®£Ø3£©¢ŁĖıߊĪOAEBŹĒĘ½ŠŠĖıߊĪ£®ĄķÓÉČē¼ū½āĪö£»¢ŚĻ߶ĪBMµÄ³¤ĪŖ
£©£®£Ø3£©¢ŁĖıߊĪOAEBŹĒĘ½ŠŠĖıߊĪ£®ĄķÓÉČē¼ū½āĪö£»¢ŚĻ߶ĪBMµÄ³¤ĪŖ![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©½«A£Ø![]() £¬0£©ŗĶB£Ø1£¬
£¬0£©ŗĶB£Ø1£¬![]() £©“śČėÅ×ĪļĻß½āĪöŹ½
£©“śČėÅ×ĪļĻß½āĪöŹ½![]() £¬µĆ£ŗ
£¬µĆ£ŗ
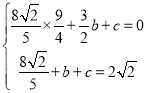 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ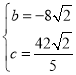 £¬
£¬
½āĪöŹ½ĪŖ£ŗ![]()
£Ø2£©µ±”ĻBDA=”ĻDACŹ±£¬BD”ĪxÖį£¬
”ßB£Ø1£¬![]() £©£¬µ±y=
£©£¬µ±y=![]() Ź±£¬
Ź±£¬![]() £¬
£¬
½āµĆ£ŗx=1»ņx=4£¬
”ąD£Ø4£¬![]() £©£¬
£©£¬
£Ø3£©¢ŁĖıߊĪOAEBŹĒĘ½ŠŠĖıߊĪ
ĄķÓÉČēĻĀ£ŗÅ×ĪļĻߵĶŌ³ĘÖįŹĒ![]() £¬
£¬
”ąBE=![]() -1=
-1=![]() £¬
£¬
”ßA£Ø![]() £¬0£©
£¬0£©
”ąOA-BE=![]()
”ßBE”ĪOA
”ąĖıߊĪOAEBŹĒĘ½ŠŠĖıߊĪ
¢Ś”ßO£Ø0£¬0£©£¬B£Ø1£¬![]() £©£¬FĪŖOBµÄÖŠµć£¬
£©£¬FĪŖOBµÄÖŠµć£¬
”ąF£Ø![]() £¬
£¬![]() £©£®
£©£®
¹żµćF×÷FN”ĶÖ±ĻßBDÓŚµćN£¬ŌņFN=![]() ©
©![]() =
=![]() £¬BN=1©
£¬BN=1©![]() =
=![]() £®
£®
ŌŚRt”÷BNFÖŠ£¬Óɹ“¹É¶ØĄķµĆ£ŗ![]() £®
£®
”ß”ĻBMF=![]() ”ĻMFO£¬”ĻMFO=”ĻFBM+”ĻBMF£¬
”ĻMFO£¬”ĻMFO=”ĻFBM+”ĻBMF£¬
”ą”ĻFBM=2”ĻBMF£®
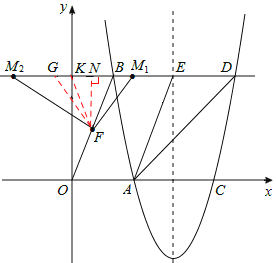
£ØI£©µ±µćMĪ»ÓŚµćBÓŅ²ąŹ±£®
ŌŚÖ±ĻßBDÉĻµćB×ó²ąČ”Ņ»µćG£¬Ź¹BG=BF=![]() £¬Į¬½ÓFG£¬ŌņGN=BG©BN=1£¬
£¬Į¬½ÓFG£¬ŌņGN=BG©BN=1£¬
ŌŚRt”÷FNGÖŠ£¬Óɹ“¹É¶ØĄķµĆ£ŗ![]() £®
£®
”ßBG=BF£¬
”ą”ĻBGF=”ĻBFG£®
Ó֔ߔĻFBM=”ĻBGF+”ĻBFG=2”ĻBMF£¬
”ą”ĻBFG=”ĻBMF£®
Ó֔ߔĻMGF=”ĻMGF£¬
”ą”÷GFB”×”÷GMF£®
”ą![]() £¬¼“
£¬¼“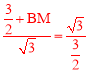 £®
£®
”ąBM=![]() £®
£®
£ØII£©µ±µćMĪ»ÓŚµćB×ó²ąŹ±£¬
ÉčBDÓėyÖį½»ÓŚµćK£¬Į¬½ÓFK£¬ŌņFKĪŖRt”÷KOBŠ±±ßÉĻµÄÖŠĻߣ¬
”ąKF=![]() OB=FB=
OB=FB=![]() £®
£®
”ą”ĻFKB=”ĻFBM=2”ĻBMF£®
Ó֔ߔĻFKB=”ĻBMF+”ĻMFK£¬
”ą”ĻBMF=”ĻMFK£®”ąMK=KF=![]() £®
£®
”ąBM=MK+BK=![]() +1=
+1=![]() £®
£®
×ŪÉĻĖłŹö£¬Ļ߶ĪBMµÄ³¤ĪŖ![]() »ņ
»ņ![]() £®
£®

 æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø
æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø ĆūĢāѵĮ·ĻµĮŠ“š°ø
ĆūĢāѵĮ·ĻµĮŠ“š°ø ĘŚÄ©¼Æ½įŗÅĻµĮŠ“š°ø
ĘŚÄ©¼Æ½įŗÅĻµĮŠ“š°ø