题目内容
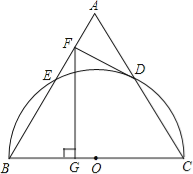
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
【答案】B
【解析】试题分析:连接OD,
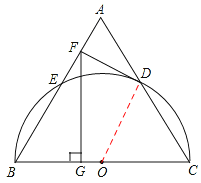
∵DF为圆O的切线,∴OD⊥DF。
∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°。
∵OD=OC,∴△OCD为等边三角形。∴OD∥AB。
又O为BC的中点,∴D为AC的中点,即OD为△ABC的中位线。
∴OD∥AB,∴DF⊥AB。
在Rt△AFD中,∠ADF=30°,AF=2,
∴AD=4,即AC=8。∴FB=AB﹣AF=8﹣2=6。
在Rt△BFG中,∠BFG=30°,∴BG=3。
则根据勾股定理得:FG=![]() 。故选B。
。故选B。

练习册系列答案
相关题目
【题目】某实验中学八年级甲.乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示:
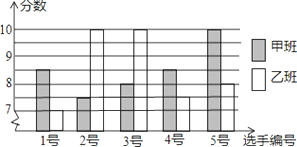
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ______ | ______ |
乙班 | 8.5 | _____ | 10 | 1.6 |
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
摸到白球的频率 |
| 0.64 | 0.58 |
| 0.60 | 0.601 |
(1)完成上表;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?