Question

【题目】如图，将两块直角三角尺的直角顶点O叠放在一起。

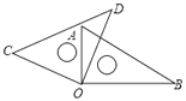
（1）若∠AOD=25°，则∠AOC= 65° ，∠BOD= ，∠BOC= ；

（2）比较∠AOC与∠BOD的大小关系，并说明理由；

（3）猜想∠AOD与∠BOC的数量关系，并说明理由。

Answer 1

【答案】（1）65°，115°；（2）∠AOC=∠BOD；理由见解析；（3）AOD+∠BOC=180°，理由见解析．

【解析】

（1）依据∠AOD+∠BOD=90°，可求得∠BOD的度数，然后依据∠BOC=∠COD+∠DOB求解即可；

（2）依据同角的余角相等进行证明即可；

（3）依据∠AOD+∠BOD+∠COD=180°求解即可．

（1）∵∠AOD=25°，

∴∠BOD=∠AOB-∠AOD=90°-25°=65°，

∠BOC=∠COD+∠DOB=90°+65°=155°

（2）∠AOC=∠BOD．

理由如下：∵∠AOC+∠AOD=90°，∠BOD+∠AOD=90°，

∴∠AOC=∠BOD．

（3）∠AOD+∠BOC=180°．

理由如下：∵∠AOB=∠COD=90°，

∴∠AOB+∠COD=180°，

又∵∠AOB=∠AOD+∠BOD，

∴∠AOD+∠BOD+∠COD=180°．

又∵∠BOD+∠COD=∠BOC，

∴∠AOD+∠BOC=180°．